Tableaux à double entrée
Dans un lycée de $2\ 000$ élèves, $55\%$ sont des garçons.
Parmi les garçons, $70\%$ font « Anglais L.V.1 » , le reste faisant « Espagnol L.V.1 ».
On sait de plus que $65\%$ des élèves de ce lycée font « Anglais L.V.1 ».
$1)$ Compléter le tableau suivant :
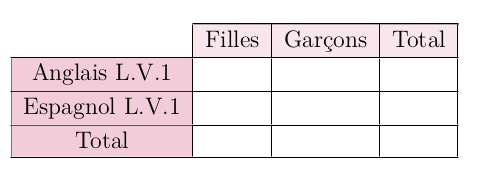
$2)$ On choisit au hasard un élève de ce lycée.
Quelle est la probabilité que ce soit un garçon faisant Anglais L.V.1 ?
$3)$ On choisit au hasard un élève de ce lycée.
Quelle est la probabilité que ce soit une fille ou que l’élève fasse Espagnol L.V.1 ?
$4)$ On choisit au hasard un élève parmi les garçons.
Quelle est la probabilité qu’il fasse Espagnol L.V.1 ?
$5)$ On choisit au hasard un élève.
Sachant que c’est une fille, quelle est la probabilité qu’elle fasse Anglais L.V.1 ?
Parmi les garçons, $70\%$ font « Anglais L.V.1 » , le reste faisant « Espagnol L.V.1 ».
On sait de plus que $65\%$ des élèves de ce lycée font « Anglais L.V.1 ».
$1)$ Compléter le tableau suivant :

$2)$ On choisit au hasard un élève de ce lycée.
Quelle est la probabilité que ce soit un garçon faisant Anglais L.V.1 ?
$3)$ On choisit au hasard un élève de ce lycée.
Quelle est la probabilité que ce soit une fille ou que l’élève fasse Espagnol L.V.1 ?
$4)$ On choisit au hasard un élève parmi les garçons.
Quelle est la probabilité qu’il fasse Espagnol L.V.1 ?
$5)$ On choisit au hasard un élève.
Sachant que c’est une fille, quelle est la probabilité qu’elle fasse Anglais L.V.1 ?

