Depuis $2010,$ le nombre de baguettes de pain fabriquées et vendues par Bonpain n'a fait qu'augmenter. Ainsi, le nombre de baguettes de pain fabriquées et vendues par semaine en $2010$ était de $200$. Il est passé à $300$ par semaine en $2012$ puis à $500$ par semaine en $2014.$ On admet que l'évolution du nombre de baguettes de pain fabriquées et vendues en une semaine par Bonpain peut être modélisé par une fonction $f$ définie sur $[0;+\infty[$ par $f(x)=ax^2+bx+c$ $($avec $a, b$ et $c$ trois nombres réels$).$
La variable $x$ désigne le nombre d'années écoullées depuis $2010$ et $f(x)$ exprime le nombre de baguettes en centaines. La valeur $0$ de $x$ correspond donc à l'année $2010.$ On cherche à déterminer la valeur des coefficients $a, b$ et $c.$
Sur le dessin ci-dessous on a représenté la fonction $f.$
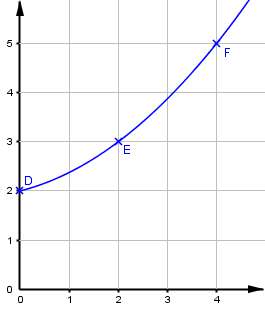
$1)$ $a.$ Donner les coordonnées de $D,E$ et $F$ puis écrire un système d'équations correspondant à cette situation.
$b.$ En déduire que le système précédent est équivalent à l'équation $MX=R$ avec $M=\begin{pmatrix}0&0&1\\4&2&1\\16&4&1\end{pmatrix}, X=\begin{pmatrix}a\\b\\c\end{pmatrix}$ et $R$ une matrice colonne que l’on précisera.
$2)$ Résoudre l’équation $MX=R$ et déterminer la valeur des coefficients $a,b$ et $c.$
Suivant ce modèle, déterminer le nombre de baguettes que l’entreprise fournira par semaine aux collectivités en $2016.$