Un triangle $ABC$ isocèle, de sommet principal $A$ est inscrit dans un cercle de centre $O$ et de rayon $1$. $H$ est le pied de la hauteur issue de $A$. On note $α$ la mesure en radian de l’angle $\widehat{HOC}$. On suppose que $0\le \alpha \le \dfrac{\pi}{2}$.



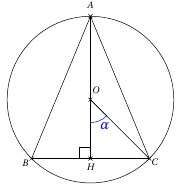
$1)$ $a.$ Exprimer $BC$ et $AH$ en fonction de $α$.


$b.$ En déduire, en fonction de $α$ l’aire du triangle $ABC.$

$2)$ On considère la fonction $f$ définie sur $\left[0;\dfrac{\pi}{2}\right]$ par $f(α)=(1+cosα)sinα.$

Montrer que $f′(α)=2cos2α+cosα–1.$

$3)$ $a.$ Factoriser le polynôme $2X^2+X−1$ et en déduire une factorisation de $f′(α).$

$b.$ Dresser le tableau de variation de $f.$

$4)$ Démontrer qu’il existe une valeur de $α$,que l’on déterminera, pour laquelle l’aire du triangle $ABC$ est maximale.
Préciser ce maximum.
Quelle est alors la nature du triangle $ABC$ $?$