Asie 2016
Soit $a$ un nombre réel compris entre $0$ et $1$. On note $f_a$ la fonction définie sur $\mathbb{R}$ par : $$f_a(x) = ae^{ax} + a.$$
On note $I(a)$ l’intégrale de la fonction $f_a$ entre $0$ et $1$ : $$I(a)=\int_{0}^{1} f(x) dx.$$
$1)$ On pose dans cette question $a = 0.$ Déterminer $I(0).$
$2)$ On pose dans cette question $a = 1.$ On étudie donc la fonction $f_1$ définie sur $\mathbb{R}$ par :
$$f_1(x) = e^x + 1.$$
$a)$ Sans étude, représenter graphiquement sur la copie la fonction $f_1$ dans un repère orthogonal et faire apparaître le nombre $I(1).$
$b)$ Calculer la valeur exacte de $I(1),$ puis arrondir au dixième.
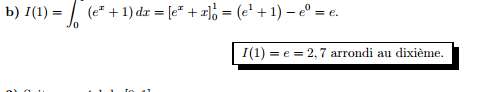
$3)$ Existe-il une valeur de a pour laquelle $I(a)$ est égale à $2$ $?$ Si oui, en donner un encadrement d’amplitude $10^{−2}.$
On note $I(a)$ l’intégrale de la fonction $f_a$ entre $0$ et $1$ : $$I(a)=\int_{0}^{1} f(x) dx.$$
$1)$ On pose dans cette question $a = 0.$ Déterminer $I(0).$
$2)$ On pose dans cette question $a = 1.$ On étudie donc la fonction $f_1$ définie sur $\mathbb{R}$ par :
$$f_1(x) = e^x + 1.$$
$a)$ Sans étude, représenter graphiquement sur la copie la fonction $f_1$ dans un repère orthogonal et faire apparaître le nombre $I(1).$
$b)$ Calculer la valeur exacte de $I(1),$ puis arrondir au dixième.
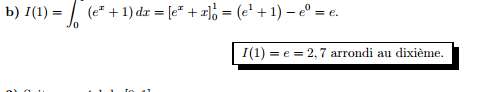
$3)$ Existe-il une valeur de a pour laquelle $I(a)$ est égale à $2$ $?$ Si oui, en donner un encadrement d’amplitude $10^{−2}.$

