La maladie cœliaque
D’après l’AFDIAG $($Association Française Des Intolérants au Gluten$),$ la maladie cœliaque, aussi appelée intolérance au gluten, est une des maladies digestives les plus fréquentes. Elle touche environ $1\%$ de la population.
On estime que seulement $20\%$ des personnes intolérantes au gluten passent le test pour être diagnostiquées.
On considère que si une personne n’est pas intolérante au gluten, elle ne passe pas le test pour être diagnostiquée.
On choisit au hasard une personne dans la population française qui compte environ $66,6$ millions d’habitants au $1^{er}$ janvier $2016.$
On considère les évènements :
• $I$ : « la personne choisie est intolérante au gluten » ;
• $T$ : « la personne choisie passe le test pour être diagnostiquée ».
$Partie$ $A$
$1)$ Recopier et compléter l’arbre de probabilités ci-dessous :
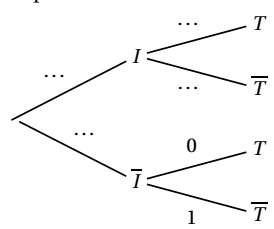
$2)$ Calculer la probabilité que la personne choisie soit intolérante au gluten et ne passe pas le test pour être diagnostiquée.
$3)$ Montrer que $p(T ) = 0,002.$
$Partie$ $B$
L’AFDIAG a fait une enquête et a constaté que la maladie cœliaque était diagnostiquée en moyenne $11$ ans après les premiers symptômes.
On note $X$ la variable aléatoire représentant le temps en années mis pour diagnostiquer la maladie cœliaque à partir de l’apparition des premiers symptômes.
On admet que la loi de $X$ peut être assimilée à la loi normale d’espérance $µ = 11$ et d’écart-type $σ = 4.$
$1)$ Calculer la probabilité que la maladie soit diagnostiquée entre $9$ ans et $13$ ans après les premiers symptômes. Arrondir le résultat à $10^{−3}.$
$2.$ Calculer $p(X \leq 6).$ Arrondir le résultat à $10^{−3}.$
$3)$ Sachant que $p(X \leq a) = 0,84,$ donner la valeur de $a$ arrondie à l’unité.
Interpréter le résultat dans le contexte de l’exercice.
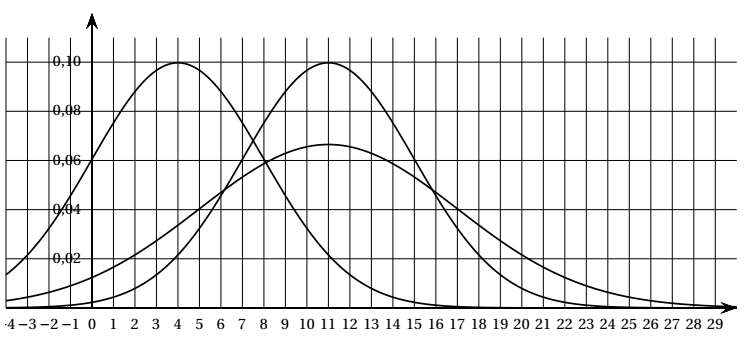
$4)$ Laquelle de ces trois courbes représente la fonction de densité de la loi normale d’espérance $µ = 11$ et d’écart-type $σ = 4$ $?$ Justifier le choix. On pourra s’aider des réponses aux questions précédentes.
On estime que seulement $20\%$ des personnes intolérantes au gluten passent le test pour être diagnostiquées.
On considère que si une personne n’est pas intolérante au gluten, elle ne passe pas le test pour être diagnostiquée.
On choisit au hasard une personne dans la population française qui compte environ $66,6$ millions d’habitants au $1^{er}$ janvier $2016.$
On considère les évènements :
• $I$ : « la personne choisie est intolérante au gluten » ;
• $T$ : « la personne choisie passe le test pour être diagnostiquée ».
$Partie$ $A$
$1)$ Recopier et compléter l’arbre de probabilités ci-dessous :

$2)$ Calculer la probabilité que la personne choisie soit intolérante au gluten et ne passe pas le test pour être diagnostiquée.
$3)$ Montrer que $p(T ) = 0,002.$
$Partie$ $B$
L’AFDIAG a fait une enquête et a constaté que la maladie cœliaque était diagnostiquée en moyenne $11$ ans après les premiers symptômes.
On note $X$ la variable aléatoire représentant le temps en années mis pour diagnostiquer la maladie cœliaque à partir de l’apparition des premiers symptômes.
On admet que la loi de $X$ peut être assimilée à la loi normale d’espérance $µ = 11$ et d’écart-type $σ = 4.$
$1)$ Calculer la probabilité que la maladie soit diagnostiquée entre $9$ ans et $13$ ans après les premiers symptômes. Arrondir le résultat à $10^{−3}.$
$2.$ Calculer $p(X \leq 6).$ Arrondir le résultat à $10^{−3}.$
$3)$ Sachant que $p(X \leq a) = 0,84,$ donner la valeur de $a$ arrondie à l’unité.
Interpréter le résultat dans le contexte de l’exercice.
$4)$ Laquelle de ces trois courbes représente la fonction de densité de la loi normale d’espérance $µ = 11$ et d’écart-type $σ = 4$ $?$ Justifier le choix. On pourra s’aider des réponses aux questions précédentes.


