Un jeu de lancer des fléchettes sur une cible. La cible est partagée en quatre secteurs, comme indiqué sur la figure ci-dessous.

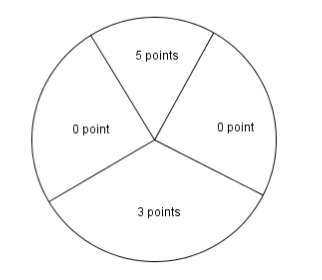
On suppose que les lancers sont indépendants et que le joueur touche la cible à tous les coups.

$1)$ Le joueur lance une fléchette. On note $p_0$ la probabilité d'obtenir $0$ points. On note $p_3$ la probabilité d'obtenir $3$ points. On note $p_5$ la probabilité d'obtenir $5$ points. On a donc $p_0+p_3+p_5=1.$ Sachant que $p_5=\frac{1}{2}p_3$ et que $p_5=\frac{1}{3}p_0$ déterminer les valeurs de $p_0, p_3$ et $p_5$.

$2)$ Une partie de ce jeu consiste à lancer trois fléchettes au maximum. Le joueur gagne la partie s'il obtient un total $($pour les $3$ lancers$)$ supérieur ou égal à $8$ points. Si au bout de $2$ lancers, il a un total supérieur ou égal à $8$ points, il ne lance pas la troisième fléchette. On note $G_2$ l'événement : « le joueur gagne la partie en $2$ lancers». On note $G_3$ l'événement : « le joueur gagne la partie en $3$ lancers». On note $P$ l'événement : « le joueur perd la partie ». On note $P(A)$ la probabilité d'un événement $A$.

$a) $ Montrer, en utilisant un arbre pondéré, que $p(G_2)=\frac{5}{36}$. On admettra dans la suite que $p(G_3)=\frac{7}{36}$.

$b)$ En déduire $p(P).$

$3)$ Un joueur joue six parties avec les règles données à la question $2.$ Quelle est la probabilité qu'il gagne au moins une partie $?$

$4)$ Pour une partie, la mise est fixée à $2$ $€$. Si le joueur gagne en deux lancers, Il reçoit $5\ €$. S'il gagne en trois lancers, il reçoit $3\ €$. S'il perd, il ne reçoit rien. On note $X$ la variable aléatoire correspondant au gain algébrique du joueur pour une partie. Les valeurs possibles pour $X$ sont donc : $-2,1$ et $3$.

$a)$ Donner la loi de probabilité de $X$.

$b)$ Déterminer l'espérance mathématique de $X$. Le jeu est-il favorable au joueur $?$