Un organisme de contrôle sanitaire s’intéresse au nombre de bactéries d’un certain type contenues dans la crème fraîche. Pour cela, il effectue des analyses portant sur $10\ 000$ prélèvements de $1\ mL$ de crème fraîche dans l’ensemble de la production française. Les résultats sont donnés dans le tableau et représentés dans l’histogramme ci-dessous :
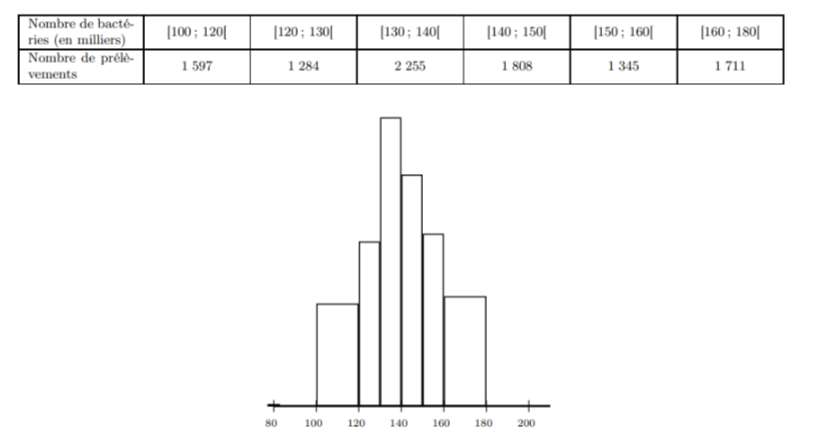
A l’aide de la calculatrice, donner une estimation de la moyenne et de l’écart-type du nombre de bactéries par prélèvement.


L’organisme décide alors de modéliser le nombre de bactéries étudiées $($en milliers par $mL)$ présentes dans la crème fraîche par une variable aléatoire $X$ suivant la loi normale de paramètres $µ = 140$ et $σ = 19.$

$1)$ $a)$ Ce choix de modélisation est-il pertinent $?$ Argumenter.

$b)$ On note $p = P(X \geq 160).$ Déterminer la valeur arrondie de $p$ à $10^{−3}.$

$2)$ Lors de l’inspection d’une laiterie, l’organisme de contrôle sanitaire analyse un échantillon de  $50$ prélèvements de $1 mL$ de crème fraîche dans la production de cette laiterie. $13$ prélèvements contiennent plus de $160$ milliers de bactéries.

$a)$ L’organisme déclare qu’il y a une anomalie dans la production et qu’il peut l’affirmer en ayant une probabilité de $0,05$ de se tromper. Justifier sa déclaration.

$b)$ Aurait-il pu l’affirmer avec une probabilité de $0, 01$ de se tromper $?$