Des études statistiques ont permis de modéliser le temps hebdomadaire, en heures, de connexion à internet des jeunes en France âgés de $16$ à $24$ ans par une variable aléatoire $T$ suivant une loi normale de moyenne $µ = 9,13$ et d’écart type $σ.$
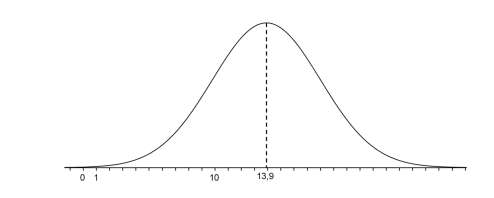
La fonction densité de probabilité de $T$ est représentée ci-dessous :

$1)$ On sait que $P(T \geq 22) = 0,023.$
En exploitant cette information :
$a.$ Hachurer, sur un graphique, deux domaines distincts
dont l’aire est égale à $0,023.$

$b.$ Déterminer $P ( 5,8 \leq T \leq 22).$ Justifier le résultat.
Montrer qu’une valeur approchée de $σ$ au dixième est $4,1.$

$2)$ On choisit un jeune en France au hasard.
Déterminer la probabilité qu’il soit connecté à internet plus de $18$ heures par semaine. Arrondir au centième.