On considère un cube $ABCDEFGH.$ On note $M$ le milieu du segment $[EH],$ $N$ celui de $[FC]$ et $P$ le point tel que $\vec{HP} = \dfrac{1}{4}\vec{HG}$ :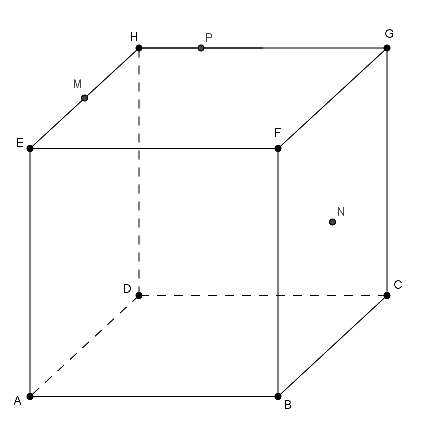
Partie A : Section du cube par le plan $(MNP)$  

$1)$ Justifier que les droites $(MP)$ et $(FG)$ sont sécantes en un point $L.$ Construire le point $L.$

$2)$ On admet que les droites $(LN)$ et $(CG)$ sont sécantes et on note $T$ leur point d’intersection. On admet que les droites $(LN)$ et $(BF)$ sont sécantes et on note $Q$ leur point d’intersection.
$a.$ Construire les points $T$ et $Q$ en laissant apparents les traits de construction.
$b.$ Construire l’intersection des plans $(MNP)$ et $(ABF).$

$3)$ En déduire une construction de la section du cube par le plan $(MNP).$