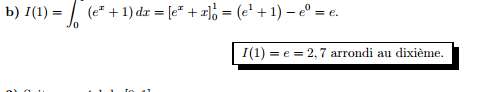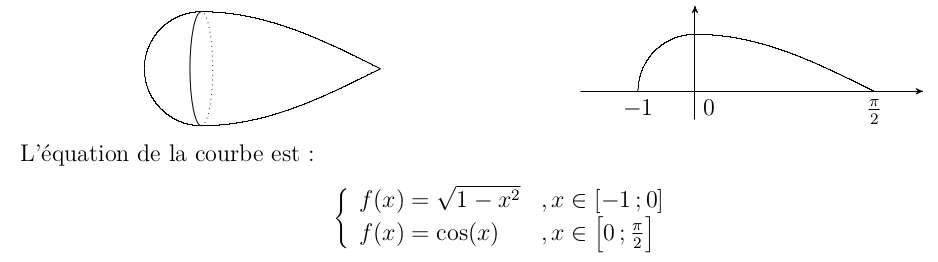Chapitres Terminale S > Analyse - Intégration

Soit $a$ un nombre réel compris entre $0$ et $1$. On note $f_a$ la fonction définie sur $\mathbb{R}$ par : $$f_a(x) = ae^{ax} + a.$$
On note $I(a)$ l’intégrale de la fonction $f_a$ entre $0$ et $1$ : $$I(a)=\int_{0}^{1} f(x) dx.$$
$1)$ On pose dans cette question $a = 0.$ Déterminer $I(0).$

$2)$ On pose dans cette question $a = 1.$ On étudie donc la fonction $f_1$ définie sur $\mathbb{R}$ par :
$$f_1(x) = e^x + 1.$$
$a)$ Sans étude, représenter graphiquement sur la copie la fonction $f_1$ dans un repère orthogonal et faire apparaître le nombre $I(1).$

$b)$ Calculer la valeur exacte de $I(1),$ puis arrondir au dixième.

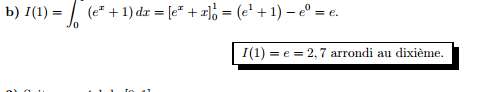
$3)$ Existe-il une valeur de a pour laquelle $I(a)$ est égale à $2$ $?$ Si oui, en donner un encadrement d’amplitude $10^{−2}.$

On considère l’intégrale : $$I=\int_{0}^{4}\sqrt{4x-x^2} .dx.$$ Montrer que $I$ représente l’aire d’un demi-disque, dont on donnera les caractéristiques, et calculer $I.$

Un bouchon de pêche est obtenu à partir d’une courbe que l’on a fait tourner autour de l’axe des abscisses.

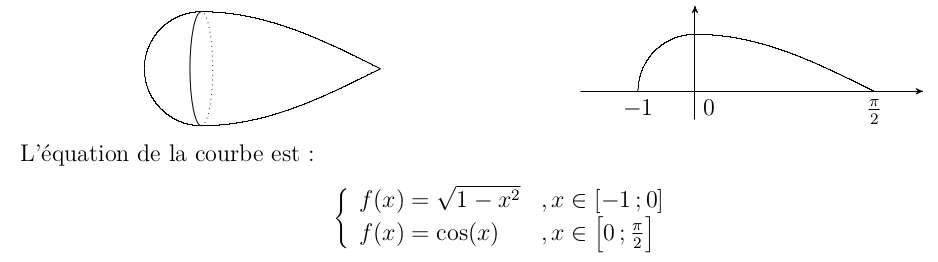
Calculer la valeur du volume $V$ du bouchon.

Calculer les intégrales proposées :

$1)$ $\int_{2}^{3} 0 .dx$ ;

$2)$ $\int_{-1}^{2} (-x+6) .dx$ ;

$3)$ $\int_{0}^{4} 2x^2+8x-1 .dx.$

Calculer les intégrales proposées :

$1)$ $\int_{0}^{\frac{2\pi}{3}} \cos x.dx$

$2)$ $\int_{1}^{3} (\dfrac{1}{x^2}) .dx$

Déterminer des primitives des fonctions $f$ suivantes, proposées sur les intervalles $I$ donnés :

$1)$ $f_1(x)=x²-5x+\dfrac{1}{x},$ sur $\ I=]0 ; +\infty [$ ;

$2)$ $f_2(x)=\dfrac{x²+x+1}{x},$ sur $I=]0 ; +\infty [.$

Soit $f$ une fonction définie par : $$f(x)=\dfrac{1}{x^3-2x²-5x+6}.$$ $1)$ Montrer que $α = 1$ est une racine du polynôme $x^3 − 2x^2 − 5x + 6.$

$2)$ En déduire ses deux autres racines, que l’on note $β$ et $γ, β < γ.$

$3)$ Déterminer les réels $A, B$ et $C$ tels que : $$f(x)=\dfrac{A}{x-\alpha}+\dfrac{B}{x-\beta}+\dfrac{C}{x-\gamma}.$$
$4)$ En déduire la valeur de $\int_{4}^{5} f(x) dx.$

Soit $a$ un nombre réel compris entre $0$ et $1.$ On note $f_a$ la fonction définie sur $\mathbb{R}$ par : $$f_a (x) = a e^{ax} + a.$$ On note $I(a)$ l’intégrale de la fonction $f_a$ entre $0$ et $1$ : $$I(a)=\int_{0}^{1} f_a(x)dx.$$ $1)$ On pose dans cette question $a = 0$. Déterminer $I(0).$

$2)$ On pose dans cette question $a = 1.$
On étudie donc la fonction $f_ 1$ définie sur $\mathbb{R}$ par : $f_1(x) = e^x +1.$
$a.$ Sans étude, représenter graphiquement sur la copie la fonction $f_1$ dans un repère orthogonal et faire apparaître le nombre $I(1).$

$b.$ Calculer la valeur exacte de $I(1),$ puis arrondir au dixième.

$3)$ Existe-il une valeur de $a$ pour laquelle $I(a)$ est égale à $2$ $?$
Si oui, en donner un encadrement d’amplitude $10^{−2}.$

Pour tout entier naturel non nul $n,$ on pose $$I_n = \displaystyle \int_0^{\frac{\pi}{4}} \left(\tan(x)\right)^n\mathrm{d}x.$$ $Partie$ $A$

$1)$ Justifier l’existence de $I_n.$

$2)$ Sans calculer $I_n,$ montrer que la suite $(I_n)$ est positive et décroissante. Que peut-on en déduire ?

$3)$ Rappeler la dérivée de la fonction $\tan,$ puis calculer celle de la fonction $h : \begin{cases} \left[0;\dfrac{\pi}{4}\right] \to \mathbb{R} \\x \mapsto \ln \left(\cos(x)\right) \end{cases}.$
En déduire les valeurs exactes de $I_1$ et $I_2.$

$4)$ En remarquant que $\left(\tan(x)\right)^3 = \tan(x) \times \left(\left(\tan(x)\right)^2+1\right) – \tan(x),$ calculer la valeur exacte de $I_3.$

Dans chacun des cas, donner l’expression algébrique d’une primitive des fonctions $f$ définies sur $\mathbb{R}$ par :

$1)$ $f(t) = 2t$ ;

$2)$ $f(t) = 3t^2$ ;

$3)$ $f(t) = 7t^6.$

Dans chacun des cas, donner l’expression algébrique d’une primitive des fonctions $f$ définies sur $\mathbb{R}$ par :

$1)$ $f(t) = 7t$ ;

$2)$ $f(t) = 6t^2$ ;

$3)$ $f(t) = 7t^5.$

Dans chacun des cas, donner l’expression algébrique d’une primitive des fonctions $f$ définies sur $\mathbb{R}$ par :

$1)$ $f(t) = 7t + 2$ ;

$2)$ $f(t) = 7t^2 – 3t + 1$ ;

$3)$ $f(t) = 6t^9 + t^2 – 3.$