Chapitres Première ES > Algèbre et Analyse - Fonction dérivée

$f$ est représentée par $C$.

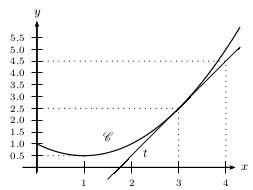
$T$ est la tangente à $C$ en $3$. Que vaut $f(1)?$

Que vaut $f′(1)\ ?$

Que vaut $f(3)\ ?$

Que vaut $f′(3)\ ?$

Déterminer une équation de la tangente $T$.

Soit $f$ la fonction définie sur $R^{*}$ par $f(x)=\dfrac{-x^{2}+2x-1}{x}$,
on note $C$ sa courbe représentative dans un repère orthonormé.

$1)$ Déterminer les abscisses des points de la courbe $C$ où la tangente est horizontale.

$2)$ Existe t'il des points de la courbe $C$ où la tangente admet un coefficient directeur égale à $-2$ $?$

$3)$ Déterminer les abscisses des points de la courbe $C$ où la tangente est parallèle à la droite d’équation $y= \dfrac{-2}{3}x-5$.

Soit $C$ la courbe représentative d'une fonction $f$ dérivable en $3$.
On sait que $f(3)=-2$ et $f'(3)=0.5.$
Écrire une équation de la tangente $T$ à $C$ au point d'abscisse $3$.

Déterminer une équation de la tangente $T$ à la courbe de la fonction $f$ au point d'abscisse $a$ dans les cas suivants :

$1)$ $f(x)=3x^{2}-x+1$, avec $a=1$.

$2)$ $f(x)=\dfrac{2x+1}{x-2}$ avec $a=3$.

$3)$ $f(x)=\dfrac{\sqrt{x}}{x}$ avec $a=9$.

Soit la fonction $ f$ définie sur $ℝ$ par $f(x)=2x^2+x-1$.
$1)$ Calculer le taux d’accroissement de $f$ entre $1$ et $1 + ℎ$ pour $ℎ ≠ 0.$

$3)$ En déduire la valeur de $f'(1)$.

Dériver les fonctions suivantes après avoir donné leur ensemble de définition et leur intervalle de dérivation : $$f(x)=\frac{4-x^2}{4x}$$

Une fonction $f$ définie sur $ [ 0; +∞[$ est représentée par la courbe $C_f$ ci-dessous. La droite $(D)$ est la droite $(OA)$.

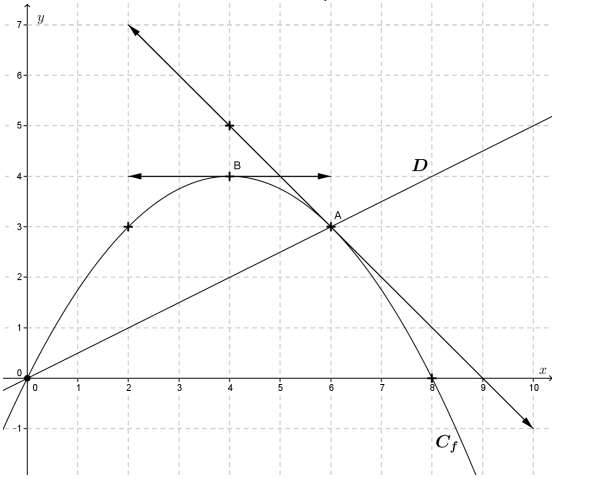
Lecture :

$a.$ Lire sur ce graphique $f(6)$ et $f′(6)$.

$b$. En déduire l’équation de la tangente à la courbe $C_f$ en $A.$

$c$. Lire $f'(4)$. Interpréter graphiquement cette lecture.

$d$. Déterminer l’équation de la droite $(D).$

Une fonction $f$ définie sur $ [ 0; +∞[$ est représentée par la courbe $C_f$ ci-dessous. La droite $(D)$ est la droite $(OA)$.

Vérification à l’aide des calculs : on admet que la fonction $f$ est donnée par : $f(x)=-0.25x^2+2x$.

$a.$ Calculer $f (6)$.

$b.$ Calculer les nombres dérivés de $f$ en $ 6$ et en $4$.

$c.$ Justifier, par un calcul, que la tangente à la courbe $C_f$ au point d’abscisse $3$ est parallèle à la droite $(D)$.

Dériver la fonction $f$ dans les cas suivants :

$1)$ $-4x^3+2x^2-3x+1$

$2)$ $\dfrac{3x^2-4x}{2}$

$3)$ $ (\sqrt{x}+1)(x^2-2)$

Dériver la fonction $f$ dans les cas suivants :

$1)$ $(2x-\sqrt{x})(x+4)$

Dériver la fonction $f$ dans les cas suivants :

$1)$ $\dfrac{2x-1}{3x+2}$

Déterminer une fonction $f$, définie sur $\mathbb{R}$, et dont la dérivée est :$$f′(x) = x^2 −3x+2.$$