Pour tout évènement $A$, on note $A$ l’évènement contraire de $A$ et $p(A)$ la probabilité de l’évènement $A.$
Si $A$ et $B$ sont deux évènements, on note $p_B(A)$ la probabilité de $A$ sachant que l’évènement $B$ est réalisé.
Dans cet exercice, on arrondira les résultats au millième.
Une agence Pôle Emploi étudie l’ensemble des demandeurs d’emploi selon deux critères, le sexe et l’expérience professionnelle.
Cette étude montre que :
• $52\%$ des demandeurs d’emploi sont des femmes et $48\%$ sont des hommes ;
• $18\%$ des demandeurs d’emploi sont sans expérience et les autres sont avec expérience ;
• parmi les hommes qui sont demandeurs d’emploi, on sait que $17,5\%$ sont sans expérience.
On prélève au hasard la fiche d’un demandeur d’emploi de cette agence. On note :
• $S$ : l’évènement « le demandeur d’emploi est sans expérience » ;
• $F$ : l’évènement « le demandeur d’emploi est une femme ».
$1)$ Préciser $p(S)$ et $p_{\bar{F}} (S).$
$2)$ Recopier l’arbre ci-dessous et compléter les pointillés par les probabilités associées.
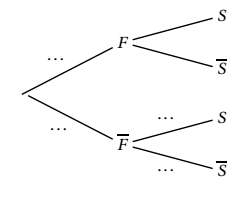
$3)$ Démontrer que $p(\bar{F} ∩S) = 0,084.$ Interpréter le résultat.
$4)$ La fiche prélevée est celle d’un demandeur d’emploi sans expérience. Calculer la probabilité pour que ce soit un homme.
$5)$ Sachant que la fiche prélevée est celle d’une femme, calculer la probabilité que ce soit la fiche d’un demandeur d’emploi sans expérience.