OQHWFM -
"Équation paramétrique de droites"
Dans chacune des questions suivantes, déterminer une équation paramétrique de la droite $D,$ passant par le point $A$ et de vecteur directeur $\overrightarrow{u}.$
Nous savons qu’une équation paramétrique de droite passant par le point $A$ $(x_A ; y_A ; z_A )$ et de vecteur directeur $\overrightarrow{u}(a,b,c)$ est définie par :
$$\left\{
\begin{array}{rcr}
x = x_A+at \\
y = y_A+bt \\
z=z_A+ct\\
\end{array}
\right.$$
$1)$ $A(0,2,-1)$ et $\overrightarrow{u}(-1,2,-1)$ ;
$2)$ $A(-3,1,5)$ et $\overrightarrow{u}(0,-2,3)$ ;
$3)$ $A(2,-3,4)$ et $\overrightarrow{u}(1,2,-3).$
|
Facile
|
0BTGDM -
"Vecteurs colinéaires dans un repère"
Pour chaque question, dire si les vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$ sont colinéaires :
$1)$ $\overrightarrow{u}=-x+5y$ et $\overrightarrow{v}=3x+2y$ ;
$2)$ $\overrightarrow{u}=-3x+7y$ et $\overrightarrow{v}=-7x+3y$ ;
$3)$ $\overrightarrow{u}=2x+3y$ et $\overrightarrow{v}=\dfrac{10}{3}x+5y.$
|
Facile
|
VFJEVX -
"Alignement de points"

$ABCD,$ $CEFD$ et $EGHF$ sont trois carrés de même côtés.
$I$ est le milieu de $[AC]$ et $J$ est le point d'intersection de $(BC)$ et $(AH).$
Montrer que $E,$ $J$ et $I$ sont alignés.
On considère le repère $(A; \overrightarrow{AB}; \overrightarrow{AD}).$
|
Facile
|
HNW5ZE -
"Coordonnées de vecteurs, colinéarité"
Dans un repère, on considère $A(-6; 1), B(3; 1), C(15;4) $ et $D(\frac{15}{2};2)$.
$1)$ Les points $A,$ $B$ et $C$ sont-ils alignés ? Justifier.
$\overrightarrow{AB}\binom{a}{b}$ et $\overrightarrow{AC}\binom{c}{d},$
$ad-bc=0.$
$\overrightarrow{AB} \;\;et\;\; \overrightarrow{AC}$ sont alignés.
$2)$ Les points $A,$ $B$ et $D$ sont-ils alignés ? Justifier.
|
Facile
|
BFSV60 -
"parallélogramme"
$ABCD$ est un parallélogramme. Soit $I$ le milieu de $[BC]$ et $J$ celui de $[CD]$. On définit alors $H$ par l'égalité $\overrightarrow{AH}=\frac{1}{3}\overrightarrow{AB }$ et $K$ par l'égalité $\overrightarrow{AK}=\frac{2}{3}\overrightarrow{AD}$.
$1)$ Faire une figure.
$2)$ Exprimer $\overrightarrow{HI}$ et $\overrightarrow{KJ}$ en fonction de $\overrightarrow{AB}$ et $\overrightarrow{AD}$.
$3)$ Les droits $(HI)$ et $(KJ)$ sont-elles parallèles $?$
|
Facile
|
8I1NUI -
"Coordonnées de vecteurs,colinéarité"
On considère un triangle $ABC$. $E$ est le symétrique de $B$ par rapport à $C$. Les points $F$ et $G$ sont définis par $\overrightarrow{AF}=\frac{3}{2}\overrightarrow{AC}$ et $\overrightarrow{BG}=-2\overrightarrow{BA}$.
$1)$ Dans le repère $(A;\overrightarrow{AB} ;\overrightarrow{AC})$, calculer les coordonnées de $E$,$F$ et $G$.
$E$ est le symétrique de $B$ par rapport à $C$ qui est le milieu de $[BE]$ : $\overrightarrow{CE}=\overrightarrow{BC}$.
$2)$ Démontrer que les points $E$,$F$ et $G$ sont alignés.
|
Facile
|
ZJDQAH -
"Amérique du Nord 2014"
On considère un cube $ABCDEFGH.$ On note $M$ le milieu du segment $[EH],$ $N$ celui de $[FC]$ et $P$ le point tel que $\vec{HP} = \dfrac{1}{4}\vec{HG}$ : 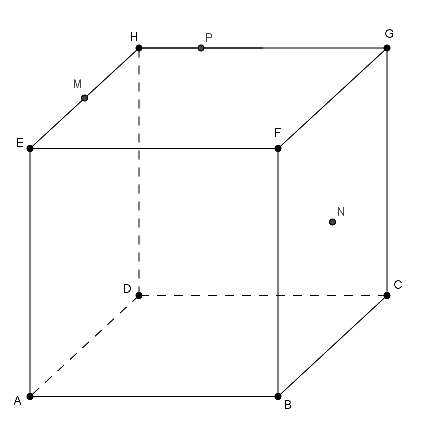
Partie A : Section du cube par le plan $(MNP)$
$1)$ Justifier que les droites $(MP)$ et $(FG)$ sont sécantes en un point $L.$ Construire le point $L.$
$2)$ On admet que les droites $(LN)$ et $(CG)$ sont sécantes et on note $T$ leur point d’intersection. On admet que les droites $(LN)$ et $(BF)$ sont sécantes et on note $Q$ leur point d’intersection.
$a.$ Construire les points $T$ et $Q$ en laissant apparents les traits de construction.
$b.$ Construire l’intersection des plans $(MNP)$ et $(ABF).$
$3)$ En déduire une construction de la section du cube par le plan $(MNP).$
|
Moyen
|
DDNN1L -
"D’après Amérique du Nord 2013"
On se place dans l’espace muni d’un repère orthonormé.
On considère les points $A(0;4;1),$ $B(1;3;0),$ $C(2;-1;-2),$ et $D(7;-1;4).$
$1)$ Démontrer que les points $A,$ $B$ et $C$ ne sont pas alignés.
$2)$ Déterminer une représentation paramétrique du plan $(ABC).$
$3)$ Déterminer une représentation paramétrique de la droite $\Delta$ passant par $D$ et de vecteur directeur $\vec{u}(2;-1;3).$
$4)$ Déterminer les coordonnées du point $H,$ intersection de la droite $Δ$ et du plan $(ABC).$
$5)$ On considère la droite $d$ dont une représentation paramétrique est \begin{cases} x=-4t-2\\y=t \qquad \qquad t\in \mathbb{R}\\z=3t+2\end{cases}
La droite $d$ et le plan $(ABC)$ sont-ils sécants ou parallèles ?
|
Moyen
|
2WAD6C -
"Antilles Guyane 2017. Enseignement spécifique"
On note $\mathbb{R}$ l’ensemble des nombres réels.
L’espace est muni d’un repère orthonormé $(O,\vec{i},\vec{j},\vec{k}).$
On considère les points $A(−1; 2; 0),$ $B(1; 2; 4)$ et $C(−1; 1; 1).$
$1)$ $a)$ Démontrer que les points $A,$ $B$ et $C$ ne sont pas alignés.
$b)$ Calculer le produit scalaire $\vec{AB}.\vec{AC}.$
$c.)$ Déterminer la mesure de l’angle $\widehat{BAC}$ arrondie au degré.
$2)$ Soit $\vec{n}$ le vecteur de coordonnées $ (2,-1,- 1).$
$a)$ Démontrer que $\vec{n}$ est un vecteur normal au plan $(ABC).$
$b)$ Déterminer une équation cartésienne du plan $(ABC).$
$3)$ Soient $\mathscr{P_1}$ le plan d’équation $3x + y − 2z + 3 = 0$ et $\mathscr{P_2}$ le plan passant par $O$ et parallèle au plan d’équation $x − 2z + 6 = 0.$
$a)$ Démontrer que le plan $\mathscr{P_2}$ a pour équation $x = 2z.$
$b)$ Démontrer que les plans $\mathscr{P_1}$ et $\mathscr{P_2}$ sont sécants.
$c)$ Soit la droite $D$ dont un système d’équations paramétriques est \begin{cases} x=2t\\\\y=-4t-3 \qquad t\in \mathbb{R}, \\\\z=t \end{cases}
Démontrer que $\mathscr{D}$ est la droite d’intersection des plans $\mathscr{P_1}$ et $\mathscr{P_2}.$
$4)$ Démontrer que la droite $\mathscr{D}$ coupe le plan $(ABC)$ en un point $I$ dont on déterminera les coordonnées.
|
Difficile
|
PEJRHB -
"Droites et plans"
On considère la pyramide $ABCDS$, où $ABCD$ est un
parallélogramme de centre $I$. Compléter, le plus précisément possible.
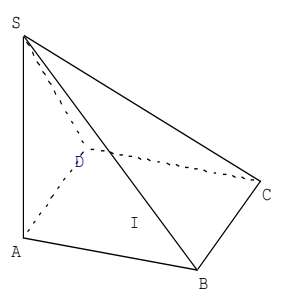
$1)$ L’intersection des plans $(SAB)$ et $(SBC)$ est …
$2)$ L’intersection des plans $(SAD)$ et $(SBC)$ est …
$3)$ L’intersection des plans $(SAB)$ et $(SCD)$ est …
$4)$ L’intersection des plans $(SAC)$ et $(SBD)$ est …
$5)$ L’intersection des plans $(SBD)$ et $(ABC)$ est …
$6)$ Les droites $(SB)$ et $(AC)$ sont …
$7)$ Les droites $(SC)$ et $(AD)$ sont …
$8)$ Les droites $(SD)$ et $(BI)$ sont …
|
Facile
|
YWIY61 -
"Droites et plans"
$ABCD$ est un tétraèdre. $I$ est un point de $[AB]$ et $J$ est un point de $[DC]$. Déterminer l’intersection des plans $(ABJ)$ et $(CDI)$ :
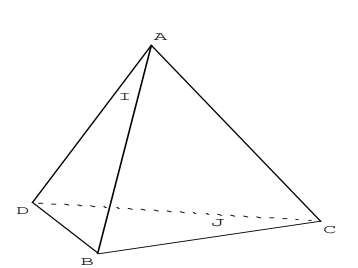
|
Facile
|
GGX8IO -
"Droites et plans"
On considère le pavé droit $ABCDEFGH$. $I$ et $ J$ sont les milieux respectifs des segments $[AD]$ et $[CD]$ :
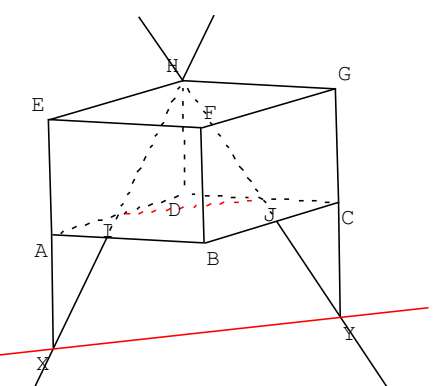
$a)$ Montrer que les droites $(HI)$ et $(EA)$ sont sécantes. On note $X$ le point d’intersection.
$b)$ Montrer que les droites $(HJ)$ et $(CG)$ sont sécantes. On note $Y$ le point d’intersection.
$c)$ Montrer que les droites $(XY)$ et $(IJ)$ sont parallèles.
|
Facile
|






