2RMC68 -
"Nouvelle Calédonie – Mars 2017 (Exo probabilité)"
Des étudiants d’une université se préparent à passer un examen pour lequel quatre thèmes $(A, B, C$ et $D)$ sont au programme.
$Partie$ $A$
Sur les $34$ sujets de l’examen déjà posés, $22$ portaient sur le thème $A.$
Peut-on rejeter au seuil de $95\%$ l’affirmation suivante : « il y a une chance sur deux que le thème $A$ soit évalué le jour de l’examen » ?
$Partie$ $B$
Le thème $A$ reste pour beaucoup d’étudiants une partie du programme difficile à maîtriser. Un stage de préparation est alors proposé pour travailler ce thème.
Lors de l’examen, on a constaté que s’il y a un exercice portant sur le thème $A$ :
• $30\%$ des étudiants n’ayant pas suivi le stage ne traitent pas l’exercice ;
• $\dfrac{5}{6}$ des étudiants ayant suivi le stage l’ont traité.
On sait de plus que $20\%$ des étudiants participent au stage.
Lors des résultats de l’examen, un étudiant s’exclame : « Je n’ai pas du tout traité le thème $A$ ».
Quelle est la probabilité que cet étudiant ait suivi le stage ? On arrondira le résultat à $0,001$ près.
$Partie$ $C$
On suppose que la variable aléatoire $T,$ associant la durée $($exprimée en minutes$)$ que consacre un étudiant de cette université pour la composition de cet examen, suit la loi normale d’espérance $µ = 225$ et d’écart-type $σ$ où $σ > 0.$
La probabilité qu’un étudiant finisse son examen en moins de $235$ minutes est de $0,98.$
Déterminer une valeur approchée de $σ$ à $0,1$ près.
On pourra, par exemple, introduire la variable aléatoire $Z=\dfrac{T-225}{\sigma}.$
|
Difficile
|
WT5Y6Y -
"PROBABILITÉS LANCERS SUCCESSIFS – BAC S PONDICHÉRY 2009"
On dispose de deux dés cubiques dont les faces sont numérotées de $1$ à $6.$ Ces dés sont en apparence identiques mais l’un est bien équilibré et l’autre truqué. Avec le dé truqué la probabilité d’obtenir $6$ lors d’un lancer est égale à $\dfrac{1}{3}.$
$1)$ On lance le dé bien équilibré trois fois de suite et on désigne par $X$ la variable aléatoire donnant le nombre de $6$ obtenus.
$a.$ On lance le dé bien équilibré trois fois de suite et on désigne par $X$ la variable aléatoire donnant le nombre de $6$ obtenus.
$b.$ Quelle est son espérance ?
$c.$ Calculer $P\left(X=2\right).$
$2)$ On choisit au hasard l’un des deux dés, les choix étant équiprobables. Et on lance le dé choisi trois fois de suite.
On considère les événements $D$ et $A$ suivants :
•ᅠᅠ $D$ : « le dé choisi est le dé bien équilibré » ;
•ᅠᅠ $A$ : « obtenir exactement deux $6$ ».
$a.$ Calculer la probabilité des événements suivants :
•ᅠᅠ « choisir le dé bien équilibré et obtenir exactement deux $6$ » ;
•ᅠᅠ « choisir le dé truqué et obtenir exactement deux $6$ ».
$($On pourra construire un arbre de probabilité$).$
$b.$ En déduire que : $p\left(A\right)=\frac{7}{48}.$
$c.$ Ayant choisi au hasard l’un des deux dés et l’ayant lancé trois fois de suite, on a obtenu exactement deux $6.$ Quelle est la probabilité d’avoir choisi le dé truqué ?
On choisit au hasard l’un des deux dés, les choix étant équiprobables, et on lance le dé $n$ fois de suite $(n$ désigne un entier naturel supérieur ou égal à $2).$
On note $B_{n}$ l’événement « obtenir au moins un $6$ parmi ces $n$ lancers successifs ».
$a.$ Déterminer, en fonction de $n,$ la probabilité $p_{n}$ de l’événement $B_{n}.$
$b.$ Calculer la limite de la suite $\left(p_{n}\right).$ Commenter ce résultat.
|
Moyen
|
0D3OZE -
"PROBABILITÉS – CONTAMINATION PAR UN VIRUS-BAC S MÉTROPOLE-2011"
Les résultats seront donnés sous forme décimale en arrondissant à $10^{-4}.$ Dans un pays, il y a $2\%$ de la population contaminée par un virus. On dispose d’un test de dépistage de ce virus qui a les propriétés suivantes :
- la probabilité qu’une personne contaminée ait un test positif est de $0,99$ $($sensibilité du test$)$ ;
- la probabilité qu’une personne non contaminée ait un test négatif est de $0,97$ $($spécificité du test$).$
On fait passer un test à une personne choisie au hasard dans cette population. On note $V$ l’évènement “la personne est contaminée par le virus” et $T$ l’évènement “le test est positif”. $\overline{V}$ et $\overline{T}$ désignent respectivement les évènements contraires de $V$ et $T.$
$1)$ $a.$ Préciser les valeurs des probabilités $P\left(V\right),P_{V}\left(T\right),P_{\overline{V}}\left(\overline{T}\right) .$ Traduire la situation à l’aide d’un arbre de probabilités.
$b.$ En déduire la probabilité de l’évènement $V \cap T.$
$2)$ Démontrer que la probabilité que le test soit positif est $0,049\ 2.$
$3)$ $a.$ Justifier par un calcul la phrase : « Si le test est positif, il n’y a qu’environ $40\%$ de “chances” que la personne soit contaminée ».
$b.$ Déterminer la probabilité qu’une personne ne soit pas contaminée par le virus sachant que son test est négatif.
|
Moyen
|
F6QAJ5 -
"probabilité"
Soient $A$ et $B$ deux évènements. On sait que : $p(A)=0,6$, $p(B)=0,5$ et $p(A∪B)=0,7.$ Déterminer $p_A(B)$ et $p_B(A).$
|
Moyen
|
ZJWXT9 -
"Un parc d’attraction"
Un parc d’attraction propose à son public un tout nouveau grand huit. Pour des raisons de sécurité, son accès n’est autorisé qu’aux personnes dont la taille est supérieure ou égale à $1,40$ $m$ et dont l’âge est compris entre $10$ et $70$ ans.
Des études statistiques sont menées pour évaluer l’affluence et la satisfaction des visiteurs pour ce manège.
On arrondira, si nécessaire, les probabilités à $10^{−4}.$
$1)$ $a.$ La taille en centimètres d’un visiteur du parc, choisi au hasard, est modélisée par la variable aléatoire $T$ qui suit la loi normale d’espérance $165$ et d’écart-type $20.$
Quelle est la probabilité qu’un visiteur ait la taille requise pour accéder à ce grand huit ?
$b.$ L’âge d’un visiteur du parc, choisi au hasard, est modélisée par la variable aléatoire $X$ qui suit la loi normale d’espérance $30$ et d’écart-type $17.$
Quelle est la probabilité qu’un visiteur ait l’âge requis pour accéder à ce grand huit ?
$c.$ Les études menées permettent d’établir que $89\%$ des visiteurs ont la taille exigées, $87\%$ ont l’âge requis mais $8\%$ n’ont ni la taille, ni l’âge obligatoires.
Quelle est alors la proportion des visiteurs vérifiant les conditions requises pour essayer la nouvelle attraction ?
$2)$ Un sondage est réalisé à la sortie du grand huit et révèle que $25\%$ des personnes ont attendu moins de $30 min$ avant de pouvoir essayer le manège. Parmi elles, $95\%$ sont satisfaites de l’attraction.
En revanche, $22\%$ des personnes ayant attendu plus de $30 min$ ne sont pas satisfaites de l’attraction.
On choisit au hasard un visiteur à sa sortie du grand huit.
On note $A $ l’événement “le visiteur a attendu plus de $30 min$” et $S$ l’événement “le visiteur est satisfait de l’attraction”.
$a.$ Montrer que la probabilité qu’un visiteur soit satisfait de l’attraction vaut $0,822\ 5.$
$b.$ Le directeur rencontre un visiteur insatisfait. Quelle est la probabilité que ce visiteur ait attendu moins de $30$ min ?
$3)$ Le directeur est soucieux de savoir si le temps d’attente, plus important les jours de grande affluence, remet en cause le taux de satisfaction des visiteurs. Pour cela, on interroge $200$ personnes au hasard à la sortie du grand huit. Parmi elles, $46$ se disent insatisfaites.
Le directeur peut-il être rassuré ?
|
Moyen
|
8T74OJ -
"Antilles Guyane – Septembre 2017 (Exo 01)"
Romane utilise deux modes de déplacement pour se déplacer entre son domicile et son lieu de travail : le vélo, ou les transports en commun.
$\text{Partie} \ A$
Lorsque la journée est ensoleillée, Romane se déplace en vélo $9$ fois sur $10.$
Lorsque la journée n’est pas ensoleillée, Romane se déplace en vélo $6$ fois sur $10.$
La probabilité qu’une journée soit ensoleillée, dans la ville où habite Romane, est notée $p.$
Pour une journée donnée, on note :
$E$ l’événement “la journée est ensoleillée”;
$V$ l’événement “Romane se déplace en vélo”.
$1)$ Construire l’arbre pondéré représentant la situation.
$2)$ Montrer que la probabilité que Romane se déplace en vélo lors d’une journée donnée est : $P(V)=0,3p+0,6.$
$3)$ On constate que dans $67,5\%$ des cas, c’est en vélo que Romane se déplace entre son domicile et son lieu de travail.
$a.$ Calculer la valeur de $p.$
$b.$ Sachant que Romane s’est déplacée en vélo, montrer que la probabilité que la journée soit ensoleillée est $\dfrac{1}{3}.$
|
Moyen
|
O18MSM -
"La maladie cœliaque"
D’après l’AFDIAG $($Association Française Des Intolérants au Gluten$),$ la maladie cœliaque, aussi appelée intolérance au gluten, est une des maladies digestives les plus fréquentes. Elle touche environ $1\%$ de la population.
On estime que seulement $20\%$ des personnes intolérantes au gluten passent le test pour être diagnostiquées.
On considère que si une personne n’est pas intolérante au gluten, elle ne passe pas le test pour être diagnostiquée.
On choisit au hasard une personne dans la population française qui compte environ $66,6$ millions d’habitants au $1^{er}$ janvier $2016.$
On considère les évènements :
• $I$ : « la personne choisie est intolérante au gluten » ;
• $T$ : « la personne choisie passe le test pour être diagnostiquée ».
$Partie$ $A$
$1)$ Recopier et compléter l’arbre de probabilités ci-dessous :
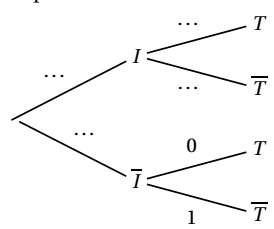
$2)$ Calculer la probabilité que la personne choisie soit intolérante au gluten et ne passe pas le test pour être diagnostiquée.
$3)$ Montrer que $p(T ) = 0,002.$
$Partie$ $B$
L’AFDIAG a fait une enquête et a constaté que la maladie cœliaque était diagnostiquée en moyenne $11$ ans après les premiers symptômes.
On note $X$ la variable aléatoire représentant le temps en années mis pour diagnostiquer la maladie cœliaque à partir de l’apparition des premiers symptômes.
On admet que la loi de $X$ peut être assimilée à la loi normale d’espérance $µ = 11$ et d’écart-type $σ = 4.$
$1)$ Calculer la probabilité que la maladie soit diagnostiquée entre $9$ ans et $13$ ans après les premiers symptômes. Arrondir le résultat à $10^{−3}.$
$2.$ Calculer $p(X \leq 6).$ Arrondir le résultat à $10^{−3}.$
$3)$ Sachant que $p(X \leq a) = 0,84,$ donner la valeur de $a$ arrondie à l’unité.
Interpréter le résultat dans le contexte de l’exercice.
$4)$ Laquelle de ces trois courbes représente la fonction de densité de la loi normale d’espérance $µ = 11$ et d’écart-type $σ = 4$ $?$ Justifier le choix. On pourra s’aider des réponses aux questions précédentes.
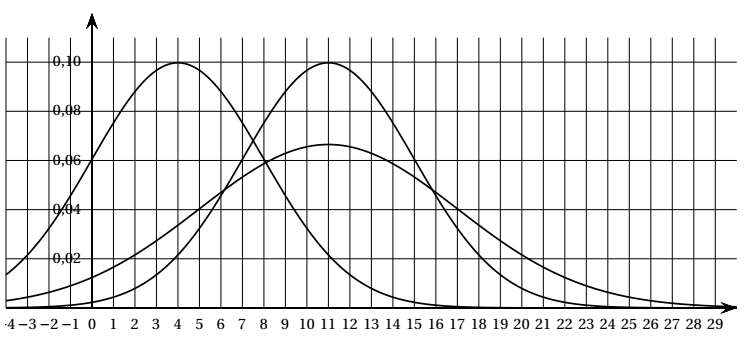
|
Moyen
|
JJ3BEC -
"Calculs de factorielles"
Calculer $\dfrac{6!}{3!}$ , $\dfrac{7!}{3!}$.
|
Facile
|
MDJVNK -
"Propriétés des nombres de combinaisons"
Pour tout nombre réel $x$ et tout entier naturel non nul $n$ : $$f(x)=(1+x)^n=1+\binom{n}{1}x^1+\binom{n}{2}x^2+\binom{n}{p}x^p+...+\binom{n}{n-1}x^{n-1}+\binom{n}{n}x^n.$$
Calculer $S=1+\binom{n}{1}+\binom{n}{2}+...+\binom{n}{p}+...+\binom{n}{n-1}+\binom{n}{n}$.
|
Facile
|
FYCMHM -
"Dénombrement en utilisant un jeu de cartes"
Dans un jeu de $32$ cartes :
$1)$ Combien y a-t-il de mains de $5$ cartes contenant $1$ roi et $2$ cœurs.
$2)$ Combien y-a-t-il de mains de $5$ cartes contenant $1$ roi et une dame et $2$ cœurs.
|
Moyen
|
O5IVW5 -
"Un jeu de lancer des fléchettes"
Un jeu de lancer des fléchettes sur une cible. La cible est partagée en quatre secteurs, comme indiqué sur la figure ci-dessous.
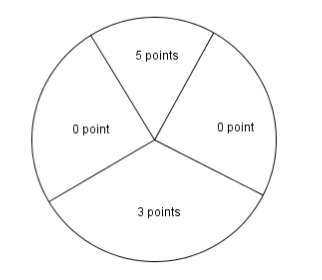
On suppose que les lancers sont indépendants et que le joueur touche la cible à tous les coups.
$1)$ Le joueur lance une fléchette. On note $p_0$ la probabilité d'obtenir $0$ points. On note $p_3$ la probabilité d'obtenir $3$ points. On note $p_5$ la probabilité d'obtenir $5$ points. On a donc $p_0+p_3+p_5=1.$ Sachant que $p_5=\frac{1}{2}p_3$ et que $p_5=\frac{1}{3}p_0$ déterminer les valeurs de $p_0, p_3$ et $p_5$.
$2)$ Une partie de ce jeu consiste à lancer trois fléchettes au maximum. Le joueur gagne la partie s'il obtient un total $($pour les $3$ lancers$)$ supérieur ou égal à $8$ points. Si au bout de $2$ lancers, il a un total supérieur ou égal à $8$ points, il ne lance pas la troisième fléchette. On note $G_2$ l'événement : « le joueur gagne la partie en $2$ lancers». On note $G_3$ l'événement : « le joueur gagne la partie en $3$ lancers». On note $P$ l'événement : « le joueur perd la partie ». On note $P(A)$ la probabilité d'un événement $A$.
$a) $ Montrer, en utilisant un arbre pondéré, que $p(G_2)=\frac{5}{36}$. On admettra dans la suite que $p(G_3)=\frac{7}{36}$.
$b)$ En déduire $p(P).$
$3)$ Un joueur joue six parties avec les règles données à la question $2.$ Quelle est la probabilité qu'il gagne au moins une partie $?$
$4)$ Pour une partie, la mise est fixée à $2$ $€$. Si le joueur gagne en deux lancers, Il reçoit $5\ €$. S'il gagne en trois lancers, il reçoit $3\ €$. S'il perd, il ne reçoit rien. On note $X$ la variable aléatoire correspondant au gain algébrique du joueur pour une partie. Les valeurs possibles pour $X$ sont donc : $-2,1$ et $3$.
$a)$ Donner la loi de probabilité de $X$.
$b)$ Déterminer l'espérance mathématique de $X$. Le jeu est-il favorable au joueur $?$
|
Moyen
|
EA86XR -
"Une urne des boules"
Une urne contient $10$ boules blanches et $n$ boules rouges, $n$ étant un entier naturel supérieur ou égal à $2$. On fait tirer à un joueur des boules de l’urne. À chaque tirage, toutes les boules ont la même probabilité d’être tirées. Pour chaque boule blanche tirée, il gagne $2$ euros et pour chaque boule rouge tirée, il perd $3$ euros. On désigne par $X$ la variable aléatoire correspondant au gain algébrique obtenu par le joueur.
$1)$ Le joueur tire deux fois successivement et sans remise une boule de l’urne.
$a)$ Démonter que $P(X = -1) = \dfrac{20n}{(n + 10)(n + 9)}.$
$b)$ Calculer, en fonction de $n$ la probabilité correspondant aux deux autres valeurs prises par la variable $X.$
$c)$ Vérifier que l’espérance mathématique de la variable aléatoire $X$ vaut : $E(X) = \dfrac{-6n^2 -14n + 360}{(n + 10)(n + 9)}.$
$d)$ Déterminer les valeurs de $n$ pour lesquelles l’espérance mathématique est strictement positive.
|
Moyen
|