Chapitres Terminale S > Proba. et statistique - Loi à densité

À un feu tricolore, le signal destiné aux piétons est vert pendant $45$ secondes et rouge pendant $105$ secondes, en alternance. À $12$ heures, le feu se met au rouge et un piéton se présente à un instant au hasard entre $12$ heures et $12$ heures $05$ pour traverser. La variable aléatoire $ T$ qui donne le temps écoulé, en secondes, entre $12$ heures et l’heure d’arrivée du piéton suit une loi uniforme sur $I = [0\ ; 300].$
Calculer la probabilité que le piéton :

$1)$ trouve le feu vert et passe sans attendre ;

$2)$ n’attende pas le feu vert plus de $15$ secondes ;

$3)$attende le feu vert plus de $30$ secondes.

Monsieur Leumateux vient d’aménager dans un quartier où se trouvent, à peu près à la même distance de chez lui, deux supermarchés, notés $A$ et $B$. Afin de choisir celui dans lequel il ira, il prend en considération le temps d’attente aux caisses.
Dans le supermarché $A,$ le temps d’attente aux caisses est une variable aléatoire $X,$ exprimée en minutes, qui suit la loi uniforme sur $[1 ; 14]$ et dans le supermarché $B,$ le temps d’attente est une variable aléatoire $Y,$ exprimée en minutes, qui suit la loi uniforme sur $[3 ; 10].$

$1)$ Déterminer la probabilité pour qu’un client attende aux caisses entre $3$ et $5$ minutes dans les deux supermarchés. Sur ce critère, quel supermarché monsieur Leumateux doit-il choisir ?

$2)$ Calculer la probabilité pour qu’un client attende eaux caisses plus de $8$ minutes dans les deux supermarchés. Sur ce critère, quel supermarché monsieur Leumateux doit-il choisir ?

$3)$ Calculer le temps d’attente moyen aux caisses pour les deux supermarchés.

À travers un sondage auprès de lycéens fréquentant un établissement en centre ville d’une grande agglomération, on constate que le temps de trajet pour se rendre de leur domicile à leur établissement est compris entre $5$ et $25$ minutes.
On interroge au hasard un lycéen d’une grande agglomération et on note $X$ la variable aléatoire égale au temps qu’il met pour aller de chez lui à son lycée.

$1)$ Donner la loi de probabilité que suit $X.$

$2)$ Quelle est la probabilité que la durée de son trajet soit comprise entre $10$ et $15$ minutes ?

$3)$ Calculer la durée moyenne du trajet domicile-lycée.

$4)$ Un élève emprunte tous les jours le même trajet pour aller de son domicile au lycée. On suppose que la durée des trajets sont indépendantes les unes des autres.
Sur une semaine de cours $($du lundi au vendredi$),$ quelle est la probabilité pour qu’au moins un trajet dure au moins $20$ minutes ? On donnera une valeur approchée au centième.

Tous les soirs, Hugo joue en ligne avec son ami Igor entre $17h30$ et $19h00.$
Caroline décide d’aller voir Hugo entre $17h00$ et et $18h00.$

$1)$ Quelle est la probabilité qu’elle dérange Hugo en pleine partie de jeu vidéo ?

$2)$ Sachant qu’elle arrive après le début du jeu, quelle est la probabilité qu’elle arrive avant $17h55$ ?

Madame Baute a commandé des chaussures sur un site Internet.
Le jour de la livraison, elle reçoit un $SMS$ lui signifiant que son colis sera livré assurément entre $10h00$ et $12h00$.
On note $X$ l’heure à laquelle elle reçoit son colis.

$1)$ Quelle est la probabilité pour que son colis arrive avant $10h15$ $?$

$2)$ Quelle est la probabilité pour que son colis arrive entre $10h30$ et $11h00$ ?

$3)$ Sachant qu’à $11h15,$ elle n’a toujours pas reçu son colis, quelle est la probabilité pour qu’elle le reçoive avant $11h30$ $?$

Hugo et Lisa se sont donnés rendez-vous entre $16h00 $ à $17h00$ sans se donner une heure précise.
Ils arriveront donc tout deux à un horaire au hasard dans cet intervalle de temps.
Hugo ne souhaite pas attendre plus de $15$ minutes et Lisa, plus de $10$ minutes, sans quoi la rencontre n’aura pas lieu.
Quelle est la probabilité qu’ils se rencontrent ?

La durée de vie d’un certain type d’appareil est modélisée par une variable aléatoire suivant une loi normale de moyenne et d’écart-type inconnus. Les spécifications impliquent que $80 \%$ de la production des appareils ait une durée de vie entre $120$ et $200$ jours et que $5 \%$ de la production ait une durée de vie inférieure à $120$ jours.

$1)$ Quelles sont les valeurs de la moyenne $μ$ et de l’écart-type $σ$ $?$

$2)$ Quelle est la probabilité d’avoir un appareil dont la durée de vie soit comprise entre $200$ jours et $230$ jours $?$

Des études statistiques ont permis de modéliser le temps hebdomadaire, en heures, de connexion à internet des jeunes en France âgés de $16$ à $24$ ans par une variable aléatoire $T$ suivant une loi normale de moyenne $µ = 9,13$ et d’écart type $σ.$
La fonction densité de probabilité de $T$ est représentée ci-dessous :

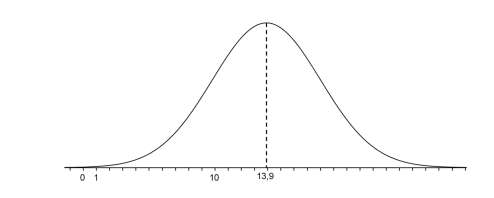
$1)$ On sait que $P(T \geq 22) = 0,023.$
En exploitant cette information :
$a.$ Hachurer, sur un graphique, deux domaines distincts
dont l’aire est égale à $0,023.$

$b.$ Déterminer $P ( 5,8 \leq T \leq 22).$ Justifier le résultat.
Montrer qu’une valeur approchée de $σ$ au dixième est $4,1.$

$2)$ On choisit un jeune en France au hasard.
Déterminer la probabilité qu’il soit connecté à internet plus de $18$ heures par semaine. Arrondir au centième.

Des étudiants d’une université se préparent à passer un examen pour lequel quatre thèmes $(A, B, C$ et $D)$ sont au programme.

$Partie$ $A$

Sur les $34$ sujets de l’examen déjà posés, $22$ portaient sur le thème $A.$
Peut-on rejeter au seuil de $95\%$ l’affirmation suivante : « il y a une chance sur deux que le thème $A$ soit évalué le jour de l’examen » ?

$Partie$ $B$

Le thème $A$ reste pour beaucoup d’étudiants une partie du programme difficile à maîtriser. Un stage de préparation est alors proposé pour travailler ce thème.
Lors de l’examen, on a constaté que s’il y a un exercice portant sur le thème $A$ :
• $30\%$ des étudiants n’ayant pas suivi le stage ne traitent pas l’exercice ;
• $\dfrac{5}{6}$ des étudiants ayant suivi le stage l’ont traité.
On sait de plus que $20\%$ des étudiants participent au stage.
Lors des résultats de l’examen, un étudiant s’exclame : « Je n’ai pas du tout traité le thème $A$ ».
Quelle est la probabilité que cet étudiant ait suivi le stage ? On arrondira le résultat à $0,001$ près.

$Partie$ $C$

On suppose que la variable aléatoire $T,$ associant la durée $($exprimée en minutes$)$ que consacre un étudiant de cette université pour la composition de cet examen, suit la loi normale d’espérance $µ = 225$ et d’écart-type $σ$ où $σ > 0.$
La probabilité qu’un étudiant finisse son examen en moins de $235$ minutes est de $0,98.$
Déterminer une valeur approchée de $σ$ à $0,1$ près.
On pourra, par exemple, introduire la variable aléatoire $Z=\dfrac{T-225}{\sigma}.$

Les résultats seront donnés sous forme décimale en arrondissant à $10^{-4}.$ Dans un pays, il y a $2\%$ de la population contaminée par un virus. On dispose d’un test de dépistage de ce virus qui a les propriétés suivantes :
- la probabilité qu’une personne contaminée ait un test positif est de $0,99$ $($sensibilité du test$)$ ;
- la probabilité qu’une personne non contaminée ait un test négatif est de $0,97$ $($spécificité du test$).$
On fait passer un test à une personne choisie au hasard dans cette population. On note $V$ l’évènement “la personne est contaminée par le virus” et $T$ l’évènement “le test est positif”. $\overline{V}$ et $\overline{T}$ désignent respectivement les évènements contraires de $V$ et $T.$
$1)$ $a.$ Préciser les valeurs des probabilités $P\left(V\right),P_{V}\left(T\right),P_{\overline{V}}\left(\overline{T}\right) .$ Traduire la situation à l’aide d’un arbre de probabilités.

$b.$ En déduire la probabilité de l’évènement $V \cap T.$

$2)$ Démontrer que la probabilité que le test soit positif est $0,049\ 2.$

$3)$ $a.$ Justifier par un calcul la phrase : « Si le test est positif, il n’y a qu’environ $40\%$ de “chances” que la personne soit contaminée ».

$b.$ Déterminer la probabilité qu’une personne ne soit pas contaminée par le virus sachant que son test est négatif.

Un parc d’attraction propose à son public un tout nouveau grand huit. Pour des raisons de sécurité, son accès n’est autorisé qu’aux personnes dont la taille est supérieure ou égale à $1,40$ $m$ et dont l’âge est compris entre $10$ et $70$ ans.
Des études statistiques sont menées pour évaluer l’affluence et la satisfaction des visiteurs pour ce manège.
On arrondira, si nécessaire, les probabilités à $10^{−4}.$

$1)$ $a.$ La taille en centimètres d’un visiteur du parc, choisi au hasard, est modélisée par la variable aléatoire $T$ qui suit la loi normale d’espérance $165$ et d’écart-type $20.$
Quelle est la probabilité qu’un visiteur ait la taille requise pour accéder à ce grand huit ?

$b.$ L’âge d’un visiteur du parc, choisi au hasard, est modélisée par la variable aléatoire $X$ qui suit la loi normale d’espérance $30$ et d’écart-type $17.$
Quelle est la probabilité qu’un visiteur ait l’âge requis pour accéder à ce grand huit ?

$c.$ Les études menées permettent d’établir que $89\%$ des visiteurs ont la taille exigées, $87\%$ ont l’âge requis mais $8\%$ n’ont ni la taille, ni l’âge obligatoires.
Quelle est alors la proportion des visiteurs vérifiant les conditions requises pour essayer la nouvelle attraction ?

$2)$ Un sondage est réalisé à la sortie du grand huit et révèle que $25\%$ des personnes ont attendu moins de $30 min$ avant de pouvoir essayer le manège. Parmi elles, $95\%$ sont satisfaites de l’attraction.
En revanche, $22\%$ des personnes ayant attendu plus de $30 min$ ne sont pas satisfaites de l’attraction.
On choisit au hasard un visiteur à sa sortie du grand huit.
On note $A $ l’événement “le visiteur a attendu plus de $30 min$” et $S$ l’événement “le visiteur est satisfait de l’attraction”.
$a.$ Montrer que la probabilité qu’un visiteur soit satisfait de l’attraction vaut $0,822\ 5.$

$b.$ Le directeur rencontre un visiteur insatisfait. Quelle est la probabilité que ce visiteur ait attendu moins de $30$ min ?

$3)$ Le directeur est soucieux de savoir si le temps d’attente, plus important les jours de grande affluence, remet en cause le taux de satisfaction des visiteurs. Pour cela, on interroge $200$ personnes au hasard à la sortie du grand huit. Parmi elles, $46$ se disent insatisfaites.
Le directeur peut-il être rassuré ?

Romane utilise deux modes de déplacement pour se déplacer entre son domicile et son lieu de travail : le vélo, ou les transports en commun.

$\text{Partie} \ A$

Lorsque la journée est ensoleillée, Romane se déplace en vélo $9$ fois sur $10.$
Lorsque la journée n’est pas ensoleillée, Romane se déplace en vélo $6$ fois sur $10.$
La probabilité qu’une journée soit ensoleillée, dans la ville où habite Romane, est notée $p.$
Pour une journée donnée, on note :
$E$ l’événement “la journée est ensoleillée”;
$V$ l’événement “Romane se déplace en vélo”.

$1)$ Construire l’arbre pondéré représentant la situation.

$2)$ Montrer que la probabilité que Romane se déplace en vélo lors d’une journée donnée est : $P(V)=0,3p+0,6.$

$3)$ On constate que dans $67,5\%$ des cas, c’est en vélo que Romane se déplace entre son domicile et son lieu de travail.
$a.$ Calculer la valeur de $p.$

$b.$ Sachant que Romane s’est déplacée en vélo, montrer que la probabilité que la journée soit ensoleillée est $\dfrac{1}{3}.$