Chapitres Terminale S > Probabilités et statistique - Estimation

Des étudiants d’une université se préparent à passer un examen pour lequel quatre thèmes $(A, B, C$ et $D)$ sont au programme.

$Partie$ $A$

Sur les $34$ sujets de l’examen déjà posés, $22$ portaient sur le thème $A.$
Peut-on rejeter au seuil de $95\%$ l’affirmation suivante : « il y a une chance sur deux que le thème $A$ soit évalué le jour de l’examen » ?

$Partie$ $B$

Le thème $A$ reste pour beaucoup d’étudiants une partie du programme difficile à maîtriser. Un stage de préparation est alors proposé pour travailler ce thème.
Lors de l’examen, on a constaté que s’il y a un exercice portant sur le thème $A$ :
• $30\%$ des étudiants n’ayant pas suivi le stage ne traitent pas l’exercice ;
• $\dfrac{5}{6}$ des étudiants ayant suivi le stage l’ont traité.
On sait de plus que $20\%$ des étudiants participent au stage.
Lors des résultats de l’examen, un étudiant s’exclame : « Je n’ai pas du tout traité le thème $A$ ».
Quelle est la probabilité que cet étudiant ait suivi le stage ? On arrondira le résultat à $0,001$ près.

$Partie$ $C$

On suppose que la variable aléatoire $T,$ associant la durée $($exprimée en minutes$)$ que consacre un étudiant de cette université pour la composition de cet examen, suit la loi normale d’espérance $µ = 225$ et d’écart-type $σ$ où $σ > 0.$
La probabilité qu’un étudiant finisse son examen en moins de $235$ minutes est de $0,98.$
Déterminer une valeur approchée de $σ$ à $0,1$ près.
On pourra, par exemple, introduire la variable aléatoire $Z=\dfrac{T-225}{\sigma}.$

Un parc d’attraction propose à son public un tout nouveau grand huit. Pour des raisons de sécurité, son accès n’est autorisé qu’aux personnes dont la taille est supérieure ou égale à $1,40$ $m$ et dont l’âge est compris entre $10$ et $70$ ans.
Des études statistiques sont menées pour évaluer l’affluence et la satisfaction des visiteurs pour ce manège.
On arrondira, si nécessaire, les probabilités à $10^{−4}.$

$1)$ $a.$ La taille en centimètres d’un visiteur du parc, choisi au hasard, est modélisée par la variable aléatoire $T$ qui suit la loi normale d’espérance $165$ et d’écart-type $20.$
Quelle est la probabilité qu’un visiteur ait la taille requise pour accéder à ce grand huit ?

$b.$ L’âge d’un visiteur du parc, choisi au hasard, est modélisée par la variable aléatoire $X$ qui suit la loi normale d’espérance $30$ et d’écart-type $17.$
Quelle est la probabilité qu’un visiteur ait l’âge requis pour accéder à ce grand huit ?

$c.$ Les études menées permettent d’établir que $89\%$ des visiteurs ont la taille exigées, $87\%$ ont l’âge requis mais $8\%$ n’ont ni la taille, ni l’âge obligatoires.
Quelle est alors la proportion des visiteurs vérifiant les conditions requises pour essayer la nouvelle attraction ?

$2)$ Un sondage est réalisé à la sortie du grand huit et révèle que $25\%$ des personnes ont attendu moins de $30 min$ avant de pouvoir essayer le manège. Parmi elles, $95\%$ sont satisfaites de l’attraction.
En revanche, $22\%$ des personnes ayant attendu plus de $30 min$ ne sont pas satisfaites de l’attraction.
On choisit au hasard un visiteur à sa sortie du grand huit.
On note $A $ l’événement “le visiteur a attendu plus de $30 min$” et $S$ l’événement “le visiteur est satisfait de l’attraction”.
$a.$ Montrer que la probabilité qu’un visiteur soit satisfait de l’attraction vaut $0,822\ 5.$

$b.$ Le directeur rencontre un visiteur insatisfait. Quelle est la probabilité que ce visiteur ait attendu moins de $30$ min ?

$3)$ Le directeur est soucieux de savoir si le temps d’attente, plus important les jours de grande affluence, remet en cause le taux de satisfaction des visiteurs. Pour cela, on interroge $200$ personnes au hasard à la sortie du grand huit. Parmi elles, $46$ se disent insatisfaites.
Le directeur peut-il être rassuré ?

D’après l’AFDIAG $($Association Française Des Intolérants au Gluten$),$ la maladie cœliaque, aussi appelée intolérance au gluten, est une des maladies digestives les plus fréquentes. Elle touche environ $1\%$ de la population.
On estime que seulement $20\%$ des personnes intolérantes au gluten passent le test pour être diagnostiquées.
On considère que si une personne n’est pas intolérante au gluten, elle ne passe pas le test pour être diagnostiquée.
On choisit au hasard une personne dans la population française qui compte environ $66,6$ millions d’habitants au $1^{er}$ janvier $2016.$
On considère les évènements :
• $I$ : « la personne choisie est intolérante au gluten » ;
• $T$ : « la personne choisie passe le test pour être diagnostiquée ».

$Partie$ $A$

$1)$ Recopier et compléter l’arbre de probabilités ci-dessous :

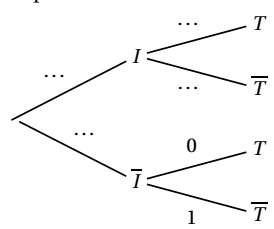
$2)$ Calculer la probabilité que la personne choisie soit intolérante au gluten et ne passe pas le test pour être diagnostiquée.

$3)$ Montrer que $p(T ) = 0,002.$

$Partie$ $B$

L’AFDIAG a fait une enquête et a constaté que la maladie cœliaque était diagnostiquée en moyenne $11$ ans après les premiers symptômes.
On note $X$ la variable aléatoire représentant le temps en années mis pour diagnostiquer la maladie cœliaque à partir de l’apparition des premiers symptômes.
On admet que la loi de $X$ peut être assimilée à la loi normale d’espérance $µ = 11$ et d’écart-type $σ = 4.$

$1)$ Calculer la probabilité que la maladie soit diagnostiquée entre $9$ ans et $13$ ans après les premiers symptômes. Arrondir le résultat à $10^{−3}.$

$2.$ Calculer $p(X \leq 6).$ Arrondir le résultat à $10^{−3}.$

$3)$ Sachant que $p(X \leq a) = 0,84,$ donner la valeur de $a$ arrondie à l’unité.
Interpréter le résultat dans le contexte de l’exercice.

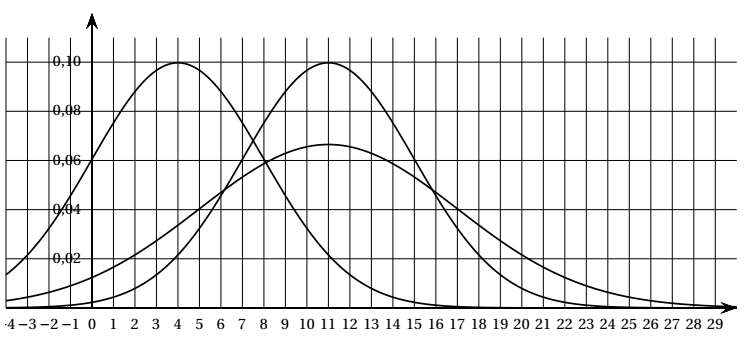
$4)$ Laquelle de ces trois courbes représente la fonction de densité de la loi normale d’espérance $µ = 11$ et d’écart-type $σ = 4$ $?$ Justifier le choix. On pourra s’aider des réponses aux questions précédentes.

Un échantillon de $10\ 000$ personnes sur une population étant donné, on sait que le taux moyen de personnes à soigner pour un manque de cholestérol est de $7,5\%$. Donner un intervalle dans lequel on soit «sûr» à $95\%$, de trouver le nombre exact de personnes à soigner sur les $10\ 000.$

Un vol Marseille - Paris est assuré par un Airbus de $150$ places, pour ce vol des estimations ont montré que la probabilité pour qu’une personne confirme son billet est $p = 0,75$. La compagnie vend $n$ billets, $n > 150.$
Soit $X$ la variable aléatoire «nombre de personnes parmi les $n$ possibles, ayant confirmé leur réservation pour ce vol».

$1)$  Quelle est la loi exacte suivie par $X$ $?$

$2)$ Quel est le nombre maximum de places que la compagnie peut vendre pour que, à au moins $95\%$, elle soit sûre que tout le monde puisse monter dans l’avion, c’est-à-dire $n$ tel que : $P[X > 150] \leq 0,05$ $?$
Reprendre le même exercice avec un avion de capacité de $300$ places; faites varier le paramètre $p = 0,5$; $p = 0,8$.

Un petit avion $($liaison Saint Brieuc-Jersey$)$ peut accueillir chaque jour $30$ personnes. Des statistiques montrent que $20\%$ des clients ayant réservé ne viennent pas. Soit $X$ la variable aléatoire : «nombre de clients qui se présentent au comptoir parmi $30$ personnes qui ont réservé».

$1)$ Quelle est la loi de $X$ $($on ne donnera que la forme générale$)$ $?$ Quelle est son espérance, son écart-type $?$

$2)$ Donner un intervalle de confiance au seuil $95\%$, permettant d’estimer le nombre de clients à prévoir.

Afin de mieux satisfaire leurs clients, une grande société fournisseur d’accès internet fait ses statistiques sur le nombre d’appels reçus en hotline, elle pourra ainsi évaluer le temps d’attente pour le client et le nombre d’employés à mettre au standard. Les résultats de l’enquête portent sur $200$ séquences consécutives de une minute, durant lesquelles le nombre d’appels moyen a été de $3$ appels par minute. On suppose que les appels sont répartis également dans le temps : on partage un intervalle de temps en unités de une seconde ; alors, dans chaque unité de temps, il y a au plus un appel.

$1)$ Quelle est la loi de probabilité du nombre d’appels reçus en $4$ minutes $?$

$2)$ Montrer que l’on peut approcher cette loi par une loi de Poisson.

$3)$ Donner un intervalle de confiance pour le nombre moyen d’appels en $4$ minutes.

Dans une usine de fabrication de composants électroniques, une chaîne de montage est destinée à la fabrication d’une carte mère. Des études précédentes, on peut admettre que si l’on choisit au hasard une carte mère fabriquée par cette chaîne de montage, la probabilité qu’elle soit défectueuse est égale à $p = 0,0125$. Le contremaître vérifie un échantillon de $1\ 000$ cartes mères à la sortie de cette chaîne. Il constate que $18$ pièces sont défectueuses.

$1)$ Déterminer l’intervalle de fluctuation au seuil de $95\%$ du nombre de pièces défectueuses fabriquées par cette chaîne de montage.

$2)$ Peut-on considérer que cette chaîne de montage doit être de nouveau réglée $?$

La société qui fabrique les fameux jeans « Clovis » avait fait faire en $2008$ une enquête de satisfaction qui indiquait que $75\%$ des clients étaient satisfaits de leur jean. Le directeur de marketing désire lancer une campagne de publicité en $2010$ dont le slogan serait « trois quarts de nos clients nous sont fidèles ».

$1)$ Sous l’hypothèse que la proportion de $2008$ est toujours valable en $2010$, déterminer l’intervalle de fluctuation au seuil de $95\%$ de la fréquence des personnes fidèles à la marque sur un échantillon de taille $100.$

$2)$ Le directeur de marketing commande une enquête à un institut de sondage auprès de $100$ personnes. L’institut répond : « $64\%$ des personnes sondées sont fidèles à la marque Clovis ». Quelle décision peut prendre le directeur de marketing $?$

Un organisme de contrôle sanitaire s’intéresse au nombre de bactéries d’un certain type contenues dans la crème fraîche. Pour cela, il effectue des analyses portant sur $10\ 000$ prélèvements de $1\ mL$ de crème fraîche dans l’ensemble de la production française. Les résultats sont donnés dans le tableau et représentés dans l’histogramme ci-dessous :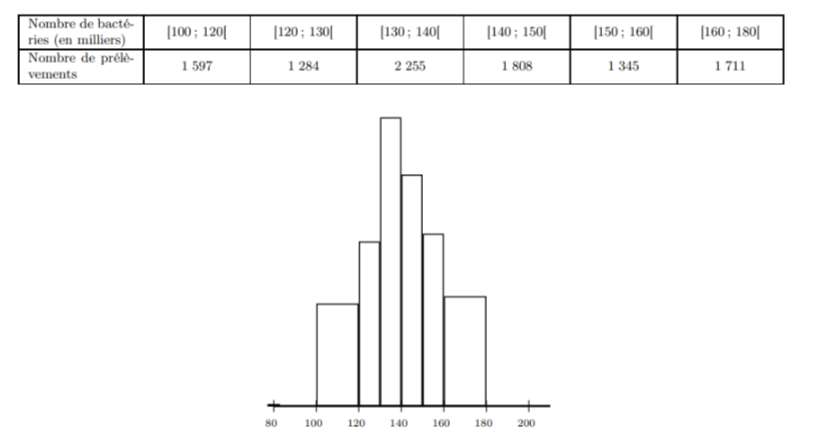
A l’aide de la calculatrice, donner une estimation de la moyenne et de l’écart-type du nombre de bactéries par prélèvement.

L’organisme décide alors de modéliser le nombre de bactéries étudiées $($en milliers par $mL)$ présentes dans la crème fraîche par une variable aléatoire $X$ suivant la loi normale de paramètres $µ = 140$ et $σ = 19.$

$1)$ $a)$ Ce choix de modélisation est-il pertinent $?$ Argumenter.

$b)$ On note $p = P(X \geq 160).$ Déterminer la valeur arrondie de $p$ à $10^{−3}.$

$2)$ Lors de l’inspection d’une laiterie, l’organisme de contrôle sanitaire analyse un échantillon de  $50$ prélèvements de $1 mL$ de crème fraîche dans la production de cette laiterie. $13$ prélèvements contiennent plus de $160$ milliers de bactéries.

$a)$ L’organisme déclare qu’il y a une anomalie dans la production et qu’il peut l’affirmer en ayant une probabilité de $0,05$ de se tromper. Justifier sa déclaration.

$b)$ Aurait-il pu l’affirmer avec une probabilité de $0, 01$ de se tromper $?$