44CN5X -
"Limites et continuité"
Soit $f$ une fonction dont le tableau de variations est :
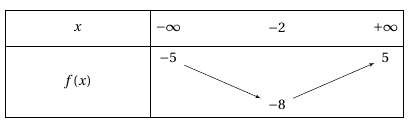
Déterminer, en justifiant, le nombre de solutions de l’équation $f(x)=0$ sur $\mathbb{R}$.
|
Facile
|
7F5G8U -
"Limites et continuité"
Soit $f$ une fonction dont le tableau de variations est :
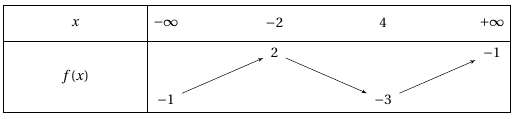
Déterminer, en justifiant, le nombre de solutions de l’équation $f(x)=0 $ sur $\mathbb{R}$.
|
Facile
|
35W85D -
"Tableau de variations"
Soit $f$ une fonction dont le tableau de variations est :
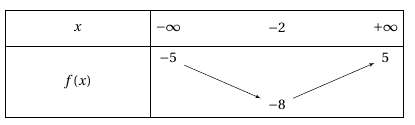
Déterminer, en justifiant, le nombre de solutions de l’équation $f(x)=0$ sur $\mathbb{R}.$
|
Moyen
|
67DKDN -
"Tableau de variations"
Soit $f$ une fonction dont le tableau de variations est :
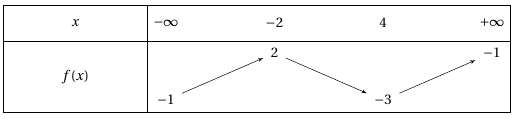
Déterminer, en justifiant, le nombre de solutions de l’équation $f(x)=0$ sur $\mathbb{R}.$
|
Moyen
|
I7U1HN -
"Tableau de variations"
Soit $f$ une fonction dont le tableau de variations est :
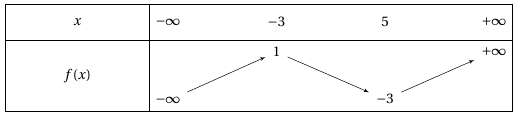
Déterminer, en justifiant, le nombre de solutions de l’équation $f(x)=1$ sur $\mathbb{R}.$
|
Moyen
|
MV1VIU -
"Fonction"
Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x) = x^3-x^2+x+2.$
$1)$ Déterminer le tableau de variations complet de la fonction $f.$
$2)$ Montrer que l’équation $f(x)=0$ ne possède qu’une unique solution notée $α.$
$3)$ Fournir un encadrement au centième de $α.$
|
Moyen
|
2Z8RV3 -
"Théorème des valeurs intermédiaire"
Soit $f$ une fonction continue sur $[0 ,1]$ et définie de $[0 ;1]$ vers $[0 ;1].$
Montrer qu’il existe $x_0$ de $[0 ,1]$ tel que $f(x_0)=x_0.$
|
Moyen
|
S01ZBV -
"Théorème des valeurs intermédiaire"
Soient $p$ et $q$ deux nombres de $\mathbb{R_+^*}$ et $f$ une fonction numérique continue sur $[0 ;1]$ tel que $f(0)≠f(1).$
Montrer qu’il existe $x_0$ de $]0 ;1[$ tels que $f(x_0)=\dfrac{pf(0)+qf(1)}{p+q}.$
On considère fonction numérique $g$ définie sur $[0,1]$ par :
$g(x)=f(x)-\dfrac{pf(0)+qf(1)}{p+q}.$
|
Difficile
|
TW1B73 -
"Théorème des valeurs intermédiaire"
Soit $f$ une onction numérique continue sur $[a,b]$ tels $f(b)>b^2$ et $f(a) < ab.$
Montrer qu’il existe $c$ de $[a,b]$ tel que $f(c)=bc.$
|
Difficile
|
YS5EW7 -
"Théorème des valeurs intermédiaires"
Soit $f$ la fonction définie sur $\mathbb{R}$ par :
$$f (x) = x^3 − 2x^2 + x − 1.$$
$1)$ Montrer que $f$ est strictement croissante sur $[1 ; 2].$
$2)$ Montrer qu’il existe une unique solution $α$ à l’équation $f (x) = 0.$
$3)$ Donnez une valeur approchée de $α$ à $0,1$ près.
|
Facile
|
SD5HN9 -
"Intersection d’une courbe avec l’axe des abscisses"
Soit $f$ la fonction définie sur $\mathbb{R}^∗$ par :
$$f(x)=\dfrac{1}{x}+x^2+x.$$
$1)$ Soit $g(x) = −1 + 2x^3 + x^2.$
Calculer $g (x),$ puis en déduire les variations de $g.$
$2)$ Montrer alors que l’équation $g(x) = 0$ admet une unique solution $α$ comprise entre $0$ et $1,$ dont on donnera une valeur approchée au millième près.
$3)$ Montrer que la courbe représentative de la fonction $f$ coupe l’axe des abscisses en un unique point, dont on donnera une valeur approchée de son abscisse au dixième près.
|
Moyen
|
3ZM3L9 -
"Graphique"
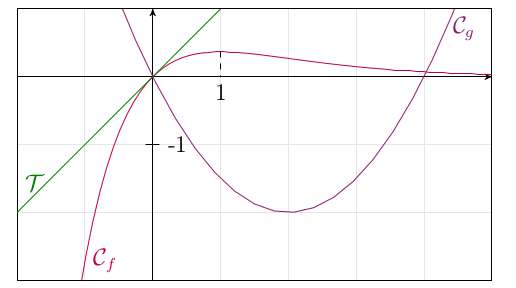
$T$ est la tangente à $C_f$ en $0.$ À l’aide du graphique ci-dessus, répondez aux questions suivantes :
$1)$ Que faut $f '(0)$ $?$ $g '(2)$ $?$
$2)$ Résoudre l’inéquation $f (x)\geq g(x)$ sur $[−2 ; 5].$
$3)$ Que semble valoir $\lim\limits_{x \to +\infty} f (x)$ $?$
|
Facile
|







