Chapitres Terminale S > Analyse - Limites de fonctions

On considère la fonction numérique définie par :
$$f(x)=\dfrac{x+x^2+...+x^n-n}{x-1}, \ \ (n \in \mathbb{N^*} )$$
$1)$ Déterminer $\lim\limits_{x \to 1} \dfrac{x^k-1}{x-1}.$

$2)$ Déduire $\lim\limits_{x \to 1} f(x).$

Soit la fonction numérique définie par :
$$f(x)=\dfrac{(1-\sin x)(1-\sin²x)...(1-sin^nx)}{\cos^{2n}x},\ \ (n\in \mathbb{N^*})$$
$1)$ Monter que : $\lim\limits_{t \to 0} \dfrac{1-\cos^kt}{1-\cos^2t}.$

$2)$ Déduire que : $\lim\limits_{x \to \frac{\pi}{2} } f(x)=\dfrac{n!}{2^n}.$

Calculer les limites suivantes :

$1)$ $ \lim\limits_{x \to - \infty} f(x)= x^2(1-\cos \frac{1}{x})$

On considère la fonction $f$ définie par $f(x)=x+\sqrt{x^2-1}$ et on note $\mathscr{C}_f$ sa courbe représentative dans un repère orthogonal.

$1)$ Quel est l’ensemble de définition $x\in\mathscr{D}_f$ de la fonction $f$ $?$

$2)$ Montrer que pour tout $x\in\mathscr{D}_f$, $f(−x)f(x)=−1.$

$3$ Déterminer la limite de $f$ en $+∞$ puis en déduire celle de $f$ en $−∞.$

$4$ Déterminer le tableau de variations de la fonction $f.$

Déterminer dans chacun des cas la limite demandée.

$1)$ $\lim\limits_{x \rightarrow -3^+} \dfrac{1}{-2x – 6}$ ;

$2)$ $\lim\limits_{x \rightarrow 0^+} \left(\left(1+\dfrac{1}{\sqrt{x}}\right) (x-3)\right)$ ;

Déterminer dans chacun des cas la limite demandée.

$1)$ $\lim\limits_{x \rightarrow 2^-} \dfrac{x^3}{4-2x}$ ;

$2$ $\lim\limits_{x \rightarrow +\infty} \dfrac{\sqrt{x} + 2 – 3x}{x}.$

Déterminer dans chacun des cas la limite demandée.

$1)$ $\lim\limits_{x \rightarrow -2^-} \dfrac{-2x}{3x+6}$ ;

$2)$ $\lim\limits_{x \rightarrow +\infty} \dfrac{2x -1}{x^2+5}$ ;

$3)$ $\lim\limits_{x \rightarrow +\infty} \dfrac{4x(-x-1)}{\left(x^2+2\right)(x+3)}.$

Déterminer dans chacun des cas la limite demandée.

$1)$ $\lim\limits_{x \rightarrow -\infty} \dfrac{x^3+2x^2}{(x+2)(x-5)}$ ;

$2)$ $\lim\limits_{x \rightarrow +\infty} \dfrac{-3x^2+5x -1}{4x^2+x+1}.$

Déterminer dans chacun des cas la limite demandée.

$1)$ $\lim\limits_{x \rightarrow -4} \dfrac{x^2+4x}{-x^2-2x+8}$ ;

$2)$ $\lim\limits_{x \rightarrow 2^+} \dfrac{x^2-4}{\sqrt{2} – \sqrt{x}}.$

Soit $f$ la fonction définie sur $\mathbb{{R}\setminus \{-2;1 \}}$ par $f(x)=\dfrac{x^2+5x+1}{x^2+x-2}.$

Combien d’asymptotes possède la courbe représentative de cette fonction ? Déterminer leur équation.

Soient $f$ la fonction définie sur $\mathbb{R\setminus\{-1;1\}}$ par $f(x) = \dfrac{3x^2-4}{x^2-1}$ et $\mathscr{C}_f$ sa courbe représentative.

$1)$ Montrer que $\mathscr{C}_f$ possède une asymptote horizontale.

$2)$ Etudier sa position relative par rapport à cette asymptote.

$3)$ Déterminer $\lim\limits_{x\rightarrow 1^-} f(x)$ et $\lim\limits_{x\rightarrow 1^+} f(x).$

$4)$ Que peut-on en déduire ?

$5)$ Existe-t-il une autre valeur pour laquelle cela soit également vrai ?

Soit $f$ une fonction dont le tableau de variations est :

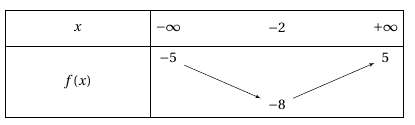
Déterminer, en justifiant, le nombre de solutions de l’équation $f(x)=0$ sur $\mathbb{R}.$