Chapitres Terminale S > Analyse - Calculs de dérivées : compléments

On considère les fonctions $f$ dérivables sur l’intervalle $I$ indiqué. Dans chacun des cas, déterminer $f′(x)$.

$1)$ $f(x) = -4x^2+56x-96, \quad I = \mathbb{R}$ ;

$2)$ $f(x) = (4x+7)(7x+10), \quad I= \mathbb{R}$ ;

$3)$ $f(x) = \dfrac{8+3x}{1-6x}, \quad I=\mathbb{R} \backslash \left\{ \dfrac{1}{6} \right\}.$

On considère les fonctions $f$ dérivables sur l’intervalle $I$ indiqué. Dans chacun des cas, déterminer $f′(x).$

$1)$ $f(x) = \dfrac{\sqrt{x}}{2 x -8}, \quad I=\mathbb{R^+} \backslash \{4 \}$ ;

$2)$ $f(x) = \dfrac{x^2+18x}{6x+4}, \quad I=\mathbb{R} \backslash \left\{-\dfrac{2}{3} \right\}.$

Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x) = \dfrac{10x+4}{5x^2+1}.$

$1)$ Déterminer pour tout $x∈\mathbb{R}$ l’expression de $f′(x)$, où $f′$ désigne la fonction dérivée de $f$.

$2)$ En déduire le sens de variation de $f$ sur $\mathbb{R}$ et dresser son tableau de variations.

$3)$ Donner l’équation de la tangente à la courbe représentant $f$ au point $A$ d’abscisse $0.$

$4)$ Étudier la position relative de cette tangente et de la courbe représentant la fonction $f.$

Dans chacun des cas suivants, justifier brièvement pourquoi la fonction $f$ est dérivable, calculer $f′(x)$ et fournir l’ensemble de dérivabilité de $f$.

$1)$ $f(x)=\dfrac{3x^2-5}{2x+3}$ ;

$2)$ $f(x)=\left(2-3x^2\right)\sqrt{x}.$

$f$ est la fonction définie sur ]$1;+∞[$ par $f(x)=\sqrt{\dfrac{x^3}{x-1}}.$

Démontrer rigoureusement que $f$ est dérivable sur $]1;+∞[$ et calculer, pour tout $x$ de $]1;+∞[,$ $f′(x).$

Un triangle $ABC$ isocèle, de sommet principal $A$ est inscrit dans un cercle de centre $O$ et de rayon $1$. $H$ est le pied de la hauteur issue de $A$. On note $α$ la mesure en radian de l’angle $\widehat{HOC}$. On suppose que $0\le \alpha \le \dfrac{\pi}{2}$.

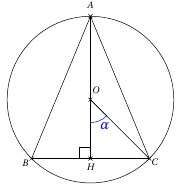
$1)$ $a.$ Exprimer $BC$ et $AH$ en fonction de $α$.

$b.$ En déduire, en fonction de $α$ l’aire du triangle $ABC.$

$2)$ On considère la fonction $f$ définie sur $\left[0;\dfrac{\pi}{2}\right]$ par $f(α)=(1+cosα)sinα.$

Montrer que $f′(α)=2cos2α+cosα–1.$

$3)$ $a.$ Factoriser le polynôme $2X^2+X−1$ et en déduire une factorisation de $f′(α).$

$b.$ Dresser le tableau de variation de $f.$

$4)$ Démontrer qu’il existe une valeur de $α$,que l’on déterminera, pour laquelle l’aire du triangle $ABC$ est maximale.
Préciser ce maximum.
Quelle est alors la nature du triangle $ABC$ $?$

Dans chacun des cas suivants, justifier brièvement pourquoi la fonction $f$ est dérivable, calculer $f′(x)$ et fournir l’ensemble de dérivabilité de $f$.

$1)$ $f(x)=\sin(1-2x)$ ;

$2)$ $f(x)=\sqrt{2x^2+3x+4}.$

Dans chacun des cas suivants, justifier brièvement pourquoi la fonction $f$ est dérivable, calculer $f′(x)$ et fournir l’ensemble de dérivabilité de $f.$

$1)$ $f(x)=\left(6x^2+3x+7\right)^3$

$2)$ -$f(x)=\dfrac{1}{\sqrt{5x-3}}$

Dans chacun des cas suivants, justifier brièvement pourquoi la fonction $f$ est dérivable, calculer $f′(x)$ et fournir l’ensemble de dérivabilité de $f.$

$1)$ $f(x)=\dfrac{1}{2x^2-1}$

$2)$ $f(x)=\dfrac{1-\sin x}{3+\cos x}$

Dans chacun des cas suivants, justifier brièvement pourquoi la fonction $f$ est dérivable, calculer $f′(x)$ et fournir l’ensemble de dérivabilité de $f.$

$1)$ $f(x)=\cos^5 x$

$2)$ $f(x)=\sqrt{\dfrac{3x}{2-x}}$

On considère la fonction $f$ définie par $f(x)=x+\sqrt{x^2-1}$ et on note $\mathscr{C}_f$ sa courbe représentative dans un repère orthogonal.

$1)$ Quel est l’ensemble de définition $x\in\mathscr{D}_f$ de la fonction $f$ $?$

$2)$ Montrer que pour tout $x\in\mathscr{D}_f$, $f(−x)f(x)=−1.$

$3$ Déterminer la limite de $f$ en $+∞$ puis en déduire celle de $f$ en $−∞.$

$4$ Déterminer le tableau de variations de la fonction $f.$

Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x) = x^3-x^2+x+2.$

$1)$ Déterminer le tableau de variations complet de la fonction $f.$

$2)$ Montrer que l’équation $f(x)=0$ ne possède qu’une unique solution notée $α.$

$3)$ Fournir un encadrement au centième de $α.$